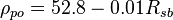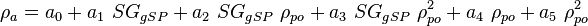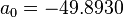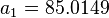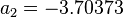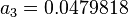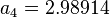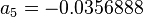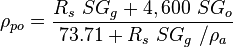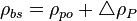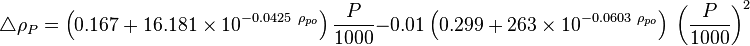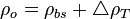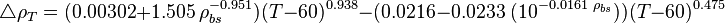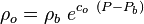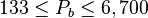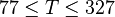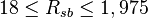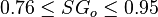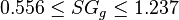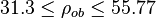McCain Oil density correlation

McCain Oil density correlation

McCain correlation is an empirical correlation for the oil density published in 1995 .

McCain oil density correlation in the PVT Software

Math & Physics

Pseudoliquid density:

$\rho_{po} = 52.8 - 0.01 R_{sb}$

Apparent liquid density:

$\rho_a = a_0 + a_1\ SG_{gSP} + a_2\ SG_{gSP}\ \rho_{po} + a_3\ SG_{gSP}\ \rho_{po}^2 + a_4\ \rho_{po} +a_5\ \rho_{po}^2$

$a_0 = -49.8930$

$a_1 = 85.0149$

$a_2 = - 3.70373$

$a_3 = 0.0479818$

$a_4 = 2.98914$

$a_5 =- 0.0356888$

Next pseudoliquid density:

$\rho_{po} = \frac{R_s\ SG_g + 4,600\ SG_o}{73.71+R_s\ SG_g\ / \rho_a}$

Iterate until pseudoliquid densities are equal.

Next adjust density to the pressure of interest:

$\rho_{bs} = \rho_{po} + \triangle \rho_P$

where

$\triangle \rho_{P} = \left ( 0.167 + 16.181 \times 10^{-0.0425\ \rho_{po}} \right) \frac{P}{1000} - 0.01 \left ( 0.299 + 263 \times 10^{-0.0603\ \rho_{po}}\right)\ \left (\frac{P}{1000}\right)^2$

Adjust density to the temperature of interest:

$\rho_{o} = \rho_{bs} + \triangle \rho_T$

where

$\triangle \rho_T = (0.00302 + 1.505\ \rho_{bs}^{-0.951}) (T - 60)^{0.938} - (0.0216 - 0.0233\ (10^{-0.0161\ \rho_{bs}})) (T - 60)^{0.475}$

Oil density above the bubble point pressure:

$\rho_{o} = \rho_{b}\ e^{c_o\ (P - P_b)}$

Example. Calculation of the oil density

Example source

Input data

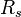$R_s$ = 53.24 sm3/sm3

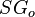$SG_o$ = 0.85 or 35 API

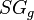$SG_g$ = 0.75

$T$ = 90C or 363K

$P$ = 10 MPa

Calculate oil density at p = 10 MPa?

Solution

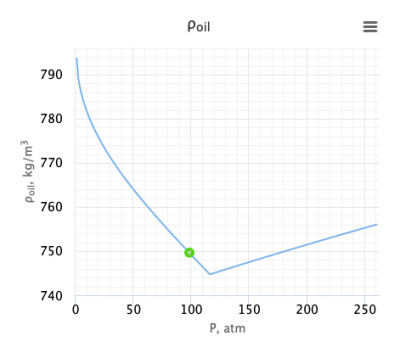
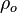$\rho_o$ = 749.645 kg/m3

The solution is available in the online PVT calculator software model at www.pengtools.com

Application range

Description of the Data Used:

$133 \le P_b \le 6,700$

$77 \le T \le 327$

$18 \le R_{sb} \le 1,975$

$0.76 \le SG_o \le 0.95$

$0.556 \le SG_g \le 1.237$

$31.3 \le \rho_{ob} \le 55.77$

Number of data sets = 684

Nomenclature

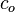$c_o$ = oil compressibility, 1/psia

$P$ = pressure, psia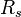

$R_s$ = solution gas-oil ratio, scf/stb

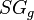$SG_g$ = gas specific gravity, dimensionless

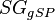$SG_{gSP}$ = gas specific gravity at separator pressure, dimensionless

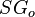$SG_o$ = oil specific gravity, dimensionless

$T$ = temperature, °F

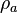$\rho_{a}$ = apparent density of surface gas if it were a liquid, lb_m/ft³

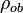$\rho_{ob}$ = liquid density at the bubble point pressure, lb_m/ft³

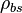$\rho_{bs}$ = liquid density at reservoir pressure and 60°F, lb_m/ft³

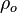$\rho_o$ = oil density, lb_m/ft³

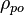$\rho_{po}$ = pseudoliquid formed by recombination of surface gas and liquid at standard conditions, lb_m/ft³

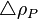$\triangle \rho_{P}$ = adjustment to liquid density due to pressure, lb_m/ft³

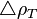$\triangle \rho_{T}$ = adjustment to liquid density due to temperature, lb_m/ft³

Subscripts

b - bubble point

g - gas

o - oil