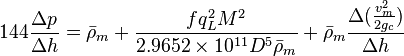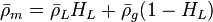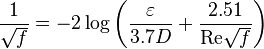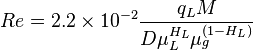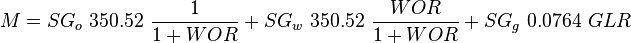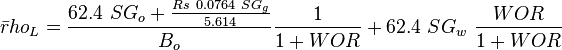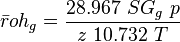Hagedorn and Brown correlation

Brief

Hagedorn and Brown is an empirical two-phase flow correlation published in 1965.

It doesn't distinguish between the flow regimes.

The heart of the Hagedorn and Brown method is a correlation for the liquid holdup :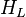$H_L$.

Math & Physics

Following the law of conservation of energy the basic steady state flow equation is:

$144 \frac{\Delta p}{\Delta h} = \bar \rho_m + \frac{f q_L^2 M^2}{2.9652 \times 10^{11} D^5 \bar \rho_m} + \bar \rho_m \frac{\Delta{(\frac{v_m^2}{2g_c}})}{\Delta h}$

where

$\bar \rho_m = \bar \rho_L H_L + \bar \rho_g (1 - H_L)$

Colebrook–White equation for the Darcy's friction factor:

$\frac{1}{\sqrt{f}}= -2 \log \left( \frac { \varepsilon} {3.7 D} + \frac {2.51} {\mathrm{Re} \sqrt{f}} \right)$

Reynolds two phase number:

$Re = 2.2 \times 10^{-2} \frac {q_L M}{D \mu_L^{H_L} \mu_g^{(1-H_L)}}$

Workflow

$M =SG_o\ 350.52\ \frac{1}{1+WOR}+SG_w\ 350.52\ \frac{WOR}{1+WOR}+SG_g\ 0.0764\ GLR$

$\bar rho_L= \frac{62.4\ SG_o + \frac{Rs\ 0.0764\ SG_g}{5.614}}{B_o} \frac{1}{1+WOR} + 62.4\ SG_w\ \frac{WOR}{1 + WOR}$

$\bar roh_g = \frac{28.967\ SG_g\ p}{z\ 10.732\ T}$