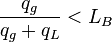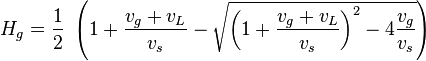Griffith correlation
From wiki.pengtools.com
Brief
The Griffith correlation [1] is an empirical correlation which defines:
- The boundary between the bubble and slug flow[2]
- The void fraction of gas in bubble flow - gas hold up Hg[2]
Math & Physics
The bubble flow exist when:
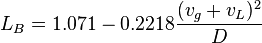 , with the limit
, with the limit 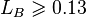 [2]
[2]
The gas holdup:
Discussion
Nomenclature
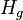 = gas holdup factor, dimensionless
= gas holdup factor, dimensionless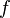 = friction factor, dimensionless
= friction factor, dimensionless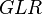 = gas-liquid ratio, scf/bbl
= gas-liquid ratio, scf/bbl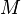 = total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl
= total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl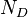 = pipe diameter number number, dimensionless
= pipe diameter number number, dimensionless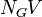 = gas velocity number, dimensionless
= gas velocity number, dimensionless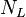 = liquid viscosity number, dimensionless
= liquid viscosity number, dimensionless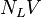 = liquid velocity number, dimensionless
= liquid velocity number, dimensionless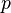 = pressure, psia
= pressure, psia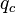 = conversion constant equal to 32.174, lbmft / lbfsec2
= conversion constant equal to 32.174, lbmft / lbfsec2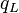 = total liquid production rate, bbl/d
= total liquid production rate, bbl/d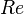 = Reynolds number, dimensionless
= Reynolds number, dimensionless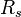 = solution gas-oil ratio, scf/stb
= solution gas-oil ratio, scf/stb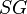 = specific gravity, dimensionless
= specific gravity, dimensionless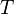 = temperature, °R or °K, follow the subscript
= temperature, °R or °K, follow the subscript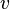 = velocity, ft/sec
= velocity, ft/sec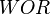 = water-oil ratio, bbl/bbl
= water-oil ratio, bbl/bbl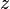 = gas compressibility factor, dimensionless
= gas compressibility factor, dimensionless
References
- ↑ Griffith, P.; Wallis, G. B. (August 1961). "Two-Phase Slug Flow"
 . Journal of Heat Transfer. ASME. 83: 307–320.
. Journal of Heat Transfer. ASME. 83: 307–320.
- ↑ 2.0 2.1 2.2 2.3 2.4 Orkiszewski, J. (June 1967). "Predicting Two-Phase Pressure Drops in Vertical Pipe"
 . Journal of Petroleum Technology. SPE. 19 (SPE-1546-PA).
. Journal of Petroleum Technology. SPE. 19 (SPE-1546-PA).