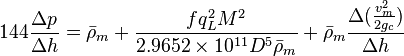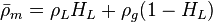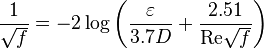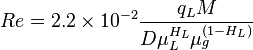Hagedorn and Brown correlation
From wiki.pengtools.com
Contents
Brief
Hagedorn and Brown is an empirical two-phase flow correlation published in 1965 [1].
It doesn't distinguish between the flow regimes.
The heart of the Hagedorn and Brown method is a correlation for the liquid holdup 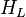 [2].
[2].
Math & Physics
Following the law of conservation of energy the basic steady state flow equation is:
where
Colebrook–White [3] equation for the Darcy's friction factor:
Reynolds two phase number:
Discussion
Why Hagedorn and Brown?
One of the consistently best correlations was found to be the empirical Hagedorn and Brown correlation. Cite error: Closing </ref> missing for <ref> tag
- ↑ 1.0 1.1 1.2 1.3 Cite error: Invalid
<ref>tag; no text was provided for refs namedHB - ↑ 2.0 2.1 Economides, M.J.; Hill, A.D.; Economides, C.E.; Zhu, D. (2013). Petroleum Production Systems (2 ed.). Westford, Massachusetts: Prentice Hall. ISBN 978-0-13-703158-0.
- ↑ 3.0 3.1 Colebrook, C. F. (1938–1939). "Turbulent Flow in Pipes, With Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws"
 . Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
. Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
- ↑ 4.0 4.1 Moody, L. F. (1944). "Friction factors for pipe flow"
 . Transactions of the ASME. 66 (8): 671–684.
. Transactions of the ASME. 66 (8): 671–684.
- ↑ Lyons, W.C. (1996). Standard handbook of petroleum and natural gas engineering. 2. Houston, TX: Gulf Professional Publishing. ISBN 0-88415-643-5.
- ↑ Trina, S. (2010). An integrated horizontal and vertical flow simulation with application to wax precipitation (Master of Engineering Thesis). Canada: Memorial University of Newfoundland.