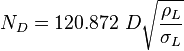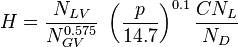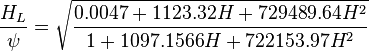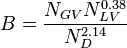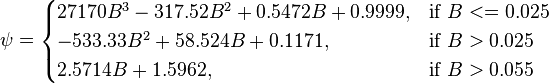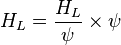Hagedorn and Brown correlation
From wiki.pengtools.com
Contents
Brief
Hagedorn and Brown is an empirical two-phase flow correlation published in 1965 [1].
It doesn't distinguish between the flow regimes.
The heart of the Hagedorn and Brown method is a correlation for the liquid holdup 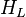 [2].
[2].
Math & Physics
Following the law of conservation of energy the basic steady state flow equation is:
where
Colebrook–White [3] equation for the Darcy's friction factor:
Reynolds two phase number:
Discussion
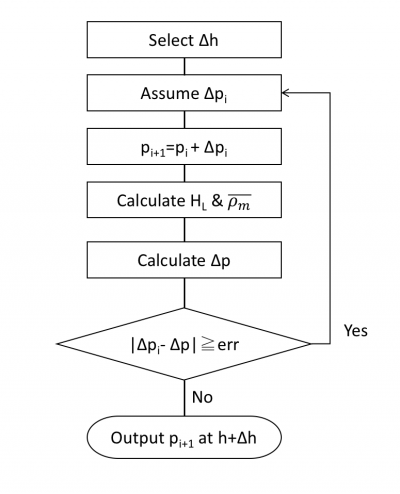
Flow Diagram
Workflow
To find 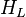 calculate:
calculate:
Nomenclature
References
Trina S. 2010. An integrated horizontal and vertical flow simulation with application to wax precipitation. Master of Engineering Thesis, Memorial University of Newfoundland, Canada.
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 Hagedorn, A. R.; Brown, K. E. (1965). "Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits". Journal of Petroleum Technology. 17(04): 475–484.
- ↑ 2.0 2.1 Economides, M.J.; Hill, A.D.; Economides, C.E.; Zhu, D. (2013). Petroleum Production Systems (2 ed.). Westford, Massachusetts: Prentice Hall. ISBN 978-0-13-703158-0.
- ↑ Colebrook, C. F. (1938–1939). "Turbulent Flow in Pipes, With Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws"
 . Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
. Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
- ↑ Moody, L. F. (1944). "Friction factors for pipe flow"
 . Transactions of the ASME. 66 (8): 671–684.
. Transactions of the ASME. 66 (8): 671–684.
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 Lyons, W.C. (1996). Standard handbook of petroleum and natural gas engineering. Pearson Education, Inc. ISBN 978-0-13-703158-0.
- ↑ 6.0 6.1 Cite error: Invalid
<ref>tag; no text was provided for refs namedTrina
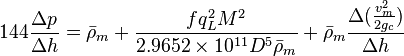
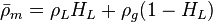
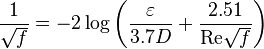
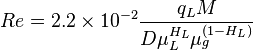
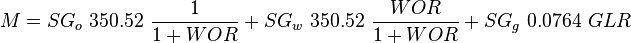
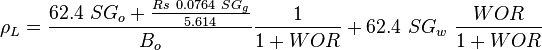
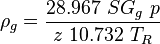
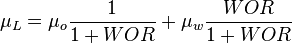
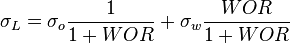
![N_L = 0.15726\ \mu_L \sqrt[4]{\frac{1}{\rho_L \sigma_L^3}}](/images/math/b/2/0/b207fe79b4a4ee53d466e182791ca737.png)
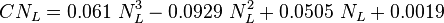
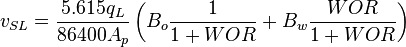
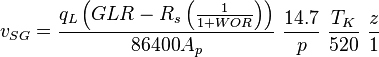
![N_{LV} = 1.938\ v_{SL}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}}](/images/math/d/d/8/dd824df0b6ec22aa724161b929e993fe.png)
![N_{GV} = 1.938\ v_{SG}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}}](/images/math/3/6/4/364153c39c1657b3b7bab8f7ed710e60.png)