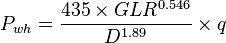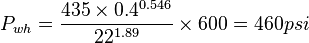Difference between revisions of "Gilbert choke equation"
From wiki.pengtools.com
(→Solution) |
|||
| Line 22: | Line 22: | ||
==Nomenclature== | ==Nomenclature== | ||
| − | :<math> | + | :<math>D</math> = choke beam diametr, 64th of an inch |
| − | + | :<math>GLR</math> = gas liquid ratio, Mscf/bbl or 10^3 scf/bbl | |
| − | + | :<math>P_{wh}</math> = well head pressure, psi | |
| − | + | :<math>q</math> = flow rate, bbl/d | |
| − | :<math> | ||
| − | |||
| − | |||
| − | :<math>P_{ | ||
| − | |||
| − | :<math> | ||
| − | |||
| − | |||
== References == | == References == | ||
Revision as of 18:47, 8 November 2024
Contents
Brief
The most common formula used for multiphase flow through surface chokes by Gilbert [1][2].
Gilbert developed his equation from field data in California.
Math and Physics
Note that the equation is independent of the downstream pressure and assumes that the downstream pressure is less than 70% of the upstream pressure.
Example
Given data
Oil rate = 600 bbl/d, GLR=400 scf/bbl, D=22/64 in, Line pressure = 180 psi
Calculate well head pressure?
Solution
Validity check 180/460=0.4 < 0.7 OK
Nomenclature
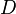 = choke beam diametr, 64th of an inch
= choke beam diametr, 64th of an inch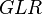 = gas liquid ratio, Mscf/bbl or 10^3 scf/bbl
= gas liquid ratio, Mscf/bbl or 10^3 scf/bbl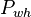 = well head pressure, psi
= well head pressure, psi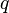 = flow rate, bbl/d
= flow rate, bbl/d
References