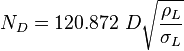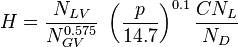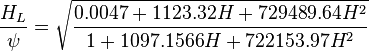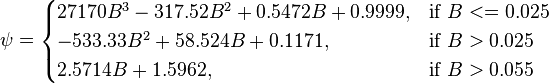Difference between revisions of "Hagedorn and Brown correlation"
From wiki.pengtools.com
(→Workflow) |
(→Workflow) |
||
| Line 33: | Line 33: | ||
:<math> \mu_L = \mu_o \frac{1}{1 + WOR} + \mu_w \frac{WOR}{1 + WOR}</math> | :<math> \mu_L = \mu_o \frac{1}{1 + WOR} + \mu_w \frac{WOR}{1 + WOR}</math> | ||
| − | :<math> \ | + | :<math> \sigma_L = \sigma_o \frac{1}{1 + WOR} + \sigma_w \frac{WOR}{1 + WOR}</math> |
:<math> N_L = 0.15726\ \mu_L \sqrt[4]{\frac{1}{\rho_L \sigma_L^3}}</math> | :<math> N_L = 0.15726\ \mu_L \sqrt[4]{\frac{1}{\rho_L \sigma_L^3}}</math> | ||
| Line 43: | Line 43: | ||
:<math> v_{SG} = \frac{q_L \left ( GLR-R_s \left( \frac{1}{1+WOR}\right) \right )}{86400 A_p}\ \frac{14.7}{p}\ \frac{T_K}{520}\ \frac{z}{1}</math> | :<math> v_{SG} = \frac{q_L \left ( GLR-R_s \left( \frac{1}{1+WOR}\right) \right )}{86400 A_p}\ \frac{14.7}{p}\ \frac{T_K}{520}\ \frac{z}{1}</math> | ||
| − | :<math> N_{LV} = 1.938\ v_{SL}\ \sqrt[4]{\frac{\rho_L}{\ | + | :<math> N_{LV} = 1.938\ v_{SL}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}} </math> |
| − | :<math> N_{GV} = 1.938\ v_{SG}\ \sqrt[4]{\frac{\rho_L}{\ | + | :<math> N_{GV} = 1.938\ v_{SG}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}} </math> |
| − | :<math> N_{D} = 120.872\ D \sqrt{\frac{\rho_L}{\ | + | :<math> N_{D} = 120.872\ D \sqrt{\frac{\rho_L}{\sigma_L}} </math> |
:<math> H = \frac{N_{LV}}{N_{GV}^{0.575}}\ \left ( \frac{p}{14.7} \right )^{0.1} \frac{CN_L}{N_D} </math> | :<math> H = \frac{N_{LV}}{N_{GV}^{0.575}}\ \left ( \frac{p}{14.7} \right )^{0.1} \frac{CN_L}{N_D} </math> | ||
Revision as of 13:41, 21 March 2017
Contents
Brief
Hagedorn and Brown is an empirical two-phase flow correlation published in 1965.
It doesn't distinguish between the flow regimes.
The heart of the Hagedorn and Brown method is a correlation for the liquid holdup :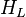 .
.
Math & Physics
Following the law of conservation of energy the basic steady state flow equation is:
where
Colebrook–White equation for the Darcy's friction factor:
Reynolds two phase number:
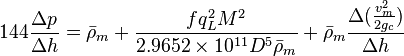
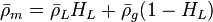
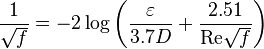
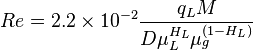
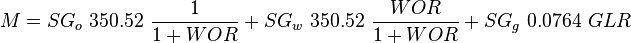
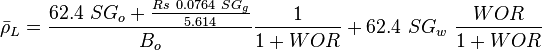
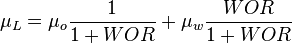
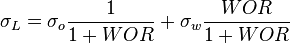
![N_L = 0.15726\ \mu_L \sqrt[4]{\frac{1}{\rho_L \sigma_L^3}}](/images/math/b/2/0/b207fe79b4a4ee53d466e182791ca737.png)
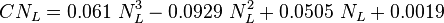
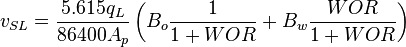
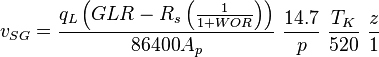
![N_{LV} = 1.938\ v_{SL}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}}](/images/math/d/d/8/dd824df0b6ec22aa724161b929e993fe.png)
![N_{GV} = 1.938\ v_{SG}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}}](/images/math/3/6/4/364153c39c1657b3b7bab8f7ed710e60.png)