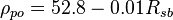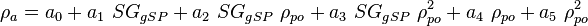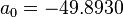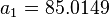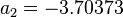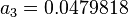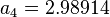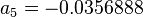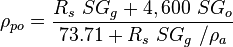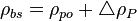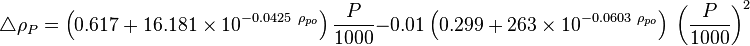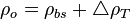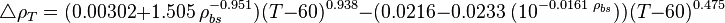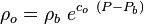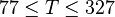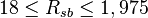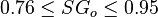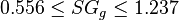Difference between revisions of "McCain Oil density correlation"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Solution)
(→‎Example. Calculation of the solution gas oil ratio)
Line 48: Line 48:
 
:<math>\rho_{o} = \rho_{b}\ e^{c_o\ (P - P_b)} </math>
 
:<math>\rho_{o} = \rho_{b}\ e^{c_o\ (P - P_b)} </math>
  
−
== Example. Calculation of the solution gas oil ratio ==
+
== Example. Calculation of the oil density ==
 
Example source <ref name=DW/>
 
Example source <ref name=DW/>
 
===Input data===
 
===Input data===
Line 59: Line 59:
  
 
===Solution===
 
===Solution===
−
:<math>/rho_o</math> = 749.645 kg/m3
+
:<math>\rho_o</math> = 749.645 kg/m3
  
−
The solution is available in the online PVT calculator software at [https://www.pengtools.com/pvtCalculator?paramsToken=de71e4cc29541ab2117e07408864410c www.pengtools.com]
+
The solution is available in the online PVT calculator software model at [https://www.pengtools.com/pvtCalculator?paramsToken=de71e4cc29541ab2117e07408864410c www.pengtools.com]
  
 
== Application range ==
 
== Application range ==

Revision as of 10:13, 28 September 2020

McCain Oil density correlation

McCain correlation is an empirical correlation for the oil density published in 1995 [1].

McCain oil density correlation in the PVT Software

Math & Physics

Pseudoliquid density:

\rho_{po} = 52.8 - 0.01 R_{sb}

Apparent liquid density:

\rho_a = a_0 + a_1\ SG_{gSP} + a_2\ SG_{gSP}\ \rho_{po} + a_3\ SG_{gSP}\ \rho_{po}^2 + a_4\ \rho_{po} +a_5\ \rho_{po}^2
a_0 = -49.8930
a_1 = 85.0149
a_2 = - 3.70373
a_3 = 0.0479818
a_4 = 2.98914
a_5 =- 0.0356888

Next pseudoliquid density:

\rho_{po} = \frac{R_s\ SG_g + 4,600\ SG_o}{73.71+R_s\ SG_g\ / \rho_a}[2]

Iterate until pseudoliquid densities are equal.

Next adjust density to the pressure of interest:

\rho_{bs} = \rho_{po} + \triangle \rho_P

where

\triangle \rho_{P} = \left ( 0.617 + 16.181 \times 10^{-0.0425\ \rho_{po}} \right) \frac{P}{1000} - 0.01 \left ( 0.299 + 263 \times 10^{-0.0603\ \rho_{po}}\right)\ \left (\frac{P}{1000}\right)^2

Adjust density to the temperature of interest:

\rho_{o} = \rho_{bs} + \triangle \rho_T

where

\triangle \rho_T = (0.00302 + 1.505\ \rho_{bs}^{-0.951}) (T - 60)^{0.938} - (0.0216 - 0.0233\ (10^{-0.0161\ \rho_{bs}})) (T - 60)^{0.475}

Oil density above the bubble point pressure:

\rho_{o} = \rho_{b}\ e^{c_o\ (P - P_b)}

Example. Calculation of the oil density

Example source [3]

Input data

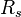R_s = 53.24 sm3/sm3
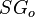SG_o = 0.85 or 35 API
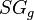SG_g = 0.75
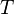T = 90C or 363K
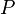P = 10 MPa

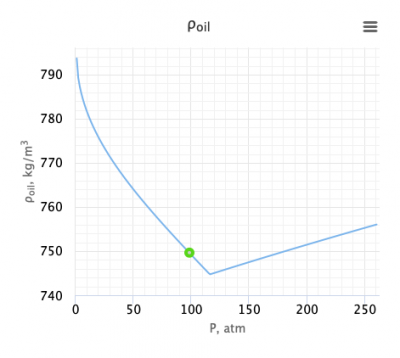
Calculate oil density at p = 10 MPa?

Solution

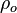\rho_o = 749.645 kg/m3

The solution is available in the online PVT calculator software model at www.pengtools.com

Application range

Description of the Data Used[1]:

133 \le P_b \le 6,700
77 \le T \le 327
18 \le R_{sb} \le 1,975
0.76 \le SG_o \le 0.95
0.556 \le SG_g \le 1.237
31.3 \le \rho_{ob} \le 55.77

Number of data sets = 684

Nomenclature

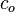c_o = oil compressibility, 1/psia
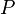P = pressure, psia
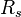R_s = solution gas-oil ratio, scf/stb
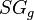SG_g = gas specific gravity, dimensionless
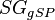SG_{gSP} = gas specific gravity at separator pressure, dimensionless
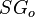SG_o = oil specific gravity, dimensionless
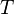T = temperature, °F
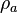\rho_{a} = apparent density of surface gas if it were a liquid, lbm/ft3
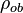\rho_{ob} = liquid density at the bubble point pressure, lbm/ft3
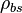\rho_{bs} = liquid density at reservoir pressure and 60°F, lbm/ft3
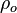\rho_o = oil density, lbm/ft3
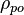\rho_{po} = pseudoliquid formed by recombination of surface gas and liquid at standard conditions, lbm/ft3
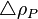\triangle \rho_{P} = adjustment to liquid density due to pressure, lbm/ft3
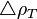\triangle \rho_{T} = adjustment to liquid density due to temperature, lbm/ft3

Subscripts

b - bubble point
g - gas
o - oil

References

  1. ↑ 1.0 1.1 McCain, W.D. Jr.; Hill, N. C. (1995). "Correlations for Liquid Densities and Evolved Gas Specific Gravities for Black Oils During Pressure Depletion"Free registration required. Society of Petroleum Engineers (SPE-30773-MS). 
  2. ↑ McCain, W.D. Jr. (1990). Properties of Petroleum Fluids (2 ed.). Oklahoma: PennWell Corp. ISBN 978-0878143351. 
  3. ↑ Cite error: Invalid <ref> tag; no text was provided for refs named DW
Retrieved from "https://wiki.pengtools.com/index.php?title=McCain_Oil_density_correlation&oldid=6972"