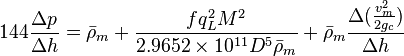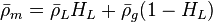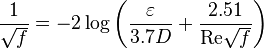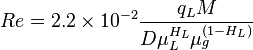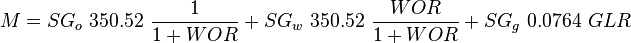Difference between revisions of "Hagedorn and Brown correlation"
From wiki.pengtools.com
(→Workflow) |
(→Workflow) |
||
| Line 22: | Line 22: | ||
:<math> M =SG_o\ 350.52\ \frac{1}{1+WOR}+SG_w\ 350.52\ \frac{WOR}{1+WOR}+SG_g\ 0.0764\ GLR</math> | :<math> M =SG_o\ 350.52\ \frac{1}{1+WOR}+SG_w\ 350.52\ \frac{WOR}{1+WOR}+SG_g\ 0.0764\ GLR</math> | ||
| + | |||
| + | :<math> \rho_L= (\frac{62.4\ SG_o + \frac{Rs\ 0.0764\ SG_g}{5.614)}{(1 + WOR)\ B_o)} + 62.4\ SG_w\ \frac{WOR}{1 + WOR}</math> | ||
== Block Diagram == | == Block Diagram == | ||
Revision as of 15:57, 20 March 2017
Brief
Hagedorn and Brown is an empirical two-phase flow correlation published in 1965.
It doesn't distinguish between the flow regimes.
The heart of the Hagedorn and Brown method is a correlation for the liquid holdup :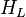 .
.
Math & Physics
Following the law of conservation of energy the basic steady state flow equation is:
where
Colebrook–White equation for the Darcy's friction factor:
Reynolds two phase number:
Workflow
- Failed to parse (syntax error): \rho_L= (\frac{62.4\ SG_o + \frac{Rs\ 0.0764\ SG_g}{5.614)}{(1 + WOR)\ B_o)} + 62.4\ SG_w\ \frac{WOR}{1 + WOR}