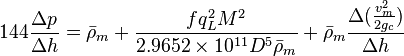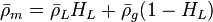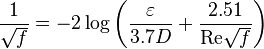Difference between revisions of "Hagedorn and Brown correlation"
From wiki.pengtools.com
(→Math & Physics) |
|||
| Line 13: | Line 13: | ||
:<math> \bar \rho_m = \bar \rho_L H_L + \bar \rho_g (1 - H_L)</math> | :<math> \bar \rho_m = \bar \rho_L H_L + \bar \rho_g (1 - H_L)</math> | ||
| − | friction factor Colebrook–White equation: | + | friction factor the Colebrook–White equation: |
:<math> \frac{1}{\sqrt{f}}= -2 \log \left( \frac { \varepsilon} {3.7 D} + \frac {2.51} {\mathrm{Re} \sqrt{f}} \right)</math> | :<math> \frac{1}{\sqrt{f}}= -2 \log \left( \frac { \varepsilon} {3.7 D} + \frac {2.51} {\mathrm{Re} \sqrt{f}} \right)</math> | ||
Revision as of 07:59, 15 March 2017
Info
Hagedorn and Brown is an empirical two-phase flow correlation published in 1965.
It doesn't distinguish between the flow regimes.
The heart of the Hagedorn and Brown method is a correlation for the liquid holdup :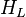 .
.
Math & Physics
The basic steady state flow equation is:
where
friction factor the Colebrook–White equation:
Workflow
For each pipe segment find: