Difference between revisions of "Category: OnPlan"

From wiki.pengtools.com
Jump to: navigation, search
Line 52: Line 52:
 
===Splitting by physical processes===
 
===Splitting by physical processes===
 
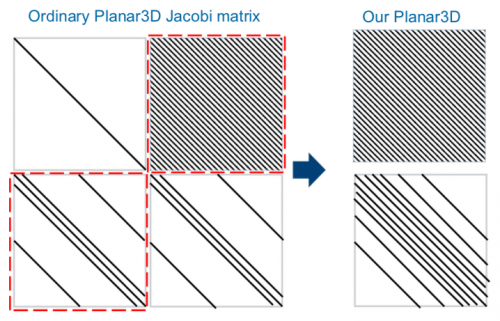
In usual numerical Planar3D implementation, Jacobi matrix includes parts that describe geomechanical and hydrodynamical processes. Splitting by physical processes allows to solve geomechanics and hydrodynamics separately. Splitting turns one linear system with dense matrix into two. Separate solving requires significantly less computation resources than solving whole system.
 
In usual numerical Planar3D implementation, Jacobi matrix includes parts that describe geomechanical and hydrodynamical processes. Splitting by physical processes allows to solve geomechanics and hydrodynamics separately. Splitting turns one linear system with dense matrix into two. Separate solving requires significantly less computation resources than solving whole system.
−
 
−
==Flow Diagram==
 
−
 
−
[[File:optiFrac flow diagram.png|400px]]
 
−
 
−
==Workflow==
 
−
 
−
[[File:Fracturedimensions.png|thumb|right|500px| Fracture Plane Dimensions]]
 
−
 
−
1. Calculate the '''N<sub>p</sub>''':
 
−
 
−
:<math>V_r=h_{net} {x_e}^2</math> the volume of the reservoir
 
−
 
−
:<math>k_f=k_{prop} * Gel Damage</math> the fracture permeability
 
−
 
−
:<math>M_f=\frac{M_{prop}}{Out Zone Growth} \frac{h_{net}}{h_{gross}}</math> the proppant mass in the pay zone
 
−
 
−
:<math>V_f=\frac{M_f}{SG_{prop} (1 - \phi_{prop})}</math> the fracture volume in the pay zone
 
−
 
−
:<math>N_p=\frac{2 k_f V_f}{k V_r}</math> the proppant number
 
−
 
−
2. Read '''C<sub>fD</sub><sup>opt</sup>''', '''I<sub>x</sub><sup>opt</sup>''', '''J<sub>D</sub><sup>opt</sup>''' from the Design Optimization Curve of the Type Curve
 
−
 
−
3. Calculate optimum fracture half-length and width:
 
−
 
−
:<math>{x_f}^{opt}=0.5 x_e {I_x}^{opt}</math>
 
−
 
−
:<math>{w_f}^{opt}=\frac{{C_{fD}}^{opt} {x_f}^{opt} k}{k_f}</math>
 
−
 
−
:<math>h_f=h_{gross} * Out Zone Growth</math> the fracture height
 
−
 
−
==Physical Constraints==
 
−
It is important to mention that the Design Optimization Curve could give unrealistic fracture geometry depending on the reservoir permeability, reservoir mechanical properties and target '''N<sub>p</sub>'''. The two most common scenarios are <ref name = pushing/>:
 
−
 
−
# The required net pressure for the fracture geometry is too high - “maximum net pressure curve”,
 
−
# Fracture width is too small (fracture too narrow) - “minimum width curve”.
 
−
 
−
 
−
The area between the “minimum width curve” and the “maximum net pressure curve” is the “working area” (highlighted in yellow) of the whole type curve for the specific rock mechanical properties, reservoir and proppant properties used. Any fracture design for this specific case should be located on the “optimum design curve” anywhere in this working area depending on the desired '''N<sub>p</sub>'''<ref name = pushing/>.
 
−
 
−
[[File:Physical Constraints on a PSS type curve.png  | link=https://www.pengtools.com/optiFrac | Open in optiFrac]]
 
−
 
−
====Maximum net pressure====
 
−
The maximum net pressure during the fracturing treatment should provide a surface pressure less than a certain value (which is surface pressure operational limit) <ref name = pushing/>.
 
−
 
−
:<math>w_{max}=\frac{2 P_{net} h_f (1 - \nu^2)}{E}</math>
 
−
 
−
:<math>w=w_{max} \frac{\pi}{4} \gamma \delta</math>
 
−
 
−
====Minimum fracture width====
 
−
Fracture propped width should be greater than N times mean proppant diameter (to provide at least N proppant layers in the fracture after closure)<ref name = pushing/>. N=3 in the [[:Category:optiFrac | optiFrac]].
 
−
 
−
== Nomenclature ==
 
−
:<math>C_{fD}</math> = dimensionless fracture conductivity, dimensionless
 
−
:<math>C_A</math> = shape factor, dimensionless
 
−
:<math>E</math> = Young's Modulus, psia
 
−
:<math>f</math> = f-function, dimensionless
 
−
:<math>Gel Damage</math> = proppant permeability reduction due to gel damage, %
 
−
:<math>h</math> = height, ft
 
−
:<math>I_x</math> = penetration ratio, dimensionless
 
−
:<math>J_D</math> = dimensionless productivity index, dimensionless
 
−
:<math>k</math> = permeability, md
 
−
:<math>M</math> = mass, lbm
 
−
:<math>N_p</math> = dimensionless proppant number, dimensionless
 
−
:<math>Out Zone Growth</math> = out of the zone growth, 0% - no growth, 50% - half of proppant is out of zone
 
−
:<math>\bar{P}_D</math> = dimensionless pressure (based on average pressure), dimensionless
 
−
:<math>P_{net}</math> = net pressure, psia
 
−
:<math>SG</math> = specific gravity, dimensionless
 
−
:<math>V</math> = volume, ft<sup>3</sup>
 
−
:<math>w</math> = width, ft
 
−
:<math>x_e</math> = drainage area, ft<sup>2</sup>
 
−
:<math>x_f</math> = fracture half-length, ft
 
−
 
−
===Greek symbols===
 
−
:<math>\delta</math> = dry to wet width ratio at the end of pumping, usually 0.5-0.7
 
−
:<math>\gamma</math> = geometric factor in vertical direction, 0.75 for PKN model, 1 for KGD model
 
−
:<math>\nu</math> = Poisson's ratio, dimensionless
 
−
:<math>\phi</math> = porosity, fraction
 
−
:<math>\pi</math> = 3.1415
 
−
 
−
===Superscripts===
 
−
:opt = optimal
 
−
:pss = pseudo-steady state
 
−
:ss = steady state
 
−
 
−
===Subscripts===
 
−
:e = external
 
−
:f = fracture
 
−
:gross = gross
 
−
:max = maximum
 
−
:net = net
 
−
:prop = proppant
 
−
:r = reservoir
 
  
 
== References ==
 
== References ==
 
<references>
 
<references>
−
<ref name= pushing >{{cite journal
 
−
|last1=Rueda|first1=J.I.
 
−
|last2=Mach|first2=J.
 
−
|last3=Wolcott|first3=D.
 
−
|title=Pushing Fracturing Limits to Maximize Producibility in Turbidite Formations in Russia
 
−
|publisher=Society of Petroleum Engineers
 
−
|number=SPE-91760-MS
 
−
|date=2004
 
−
|url=https://www.onepetro.org/conference-paper/SPE-91760-MS
 
−
|url-access=registration
 
−
}}</ref>
 
−
 
 
<ref name=UFD2002>{{cite book
 
<ref name=UFD2002>{{cite book
 
  |last1= Economides |first1= Michael J.
 
  |last1= Economides |first1= Michael J.

Revision as of 08:13, 8 October 2018

Brief

pengtools onPlan

onPlan is a fracture simulation tool for designing a hydraulic fracture treatment.

onPlan is developed under cooperation agreement between pengtools and Moscow Institute of Physics and Technology Oil&Gas Center LLC.

onPlan utilizes the Planar3D class model with advanced numerical optimization which allows to achieve high accuracy in predicting fracture geometry and fast simulation time.

onPlan integrates the Unified Fracture Design[1] concept which enables comparison of the designed frac geometry with the optimal one to maximize the performance of the fractured well.

onPlan is available online at www.pengtools.com.

Typical applications

  • Simulation of the single vertical well fractures in low stress contrast environments with a high risk of fracture breakthrough into overlying gas or underlying water
  • Optimization of hydraulic fracturing with Unified Fracture Design[1]
  • Understanding post-fracturing production performance
  • Sensitivity studies

Main features

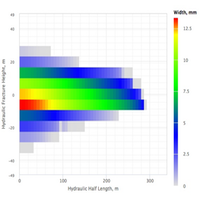
  • Fracture design charts: height, width, length, pressure vs time; height vs width; width vs length; height vs length. All showing propped and hydraulic values.
  • Fracture design Type Curves (Plot of JD as a function of CfD using Ix and Np as parameter) showing the current fracture design and the optimal one.
  • Design Optimization Curve which corresponds to the maximum JD values for different Np.
  • Design Optimum Point at which JD is maximized for the given proppant, fracture and reservoir parameters.
  • Physical constraints envelope.
  • Proppant catalog with predefined proppant properties.
  • Users reference data for benchmarking vs actual.
  • Switch between Metric and Field units
  • Save/load models to the files and to the user’s cloud
  • Share models to the public cloud or by using model’s link
  • Export pdf report containing input parameters, calculated values and plots
  • Continue your work from where you stopped: last saved model will be automatically opened
  • Download the chart as an image or data and print (upper-right corner chart’s button)
  • Export results table to Excel or other application

Math & Physics

Splitting by physical processes

Basic equations of Planar3D model:

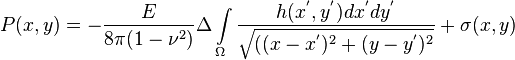P(x,y)=-\frac{E}{8\pi(1-\nu^2)}\Delta \int \limits_{\Omega}^{}\frac{h(x^', y^')dx^'dy^'}{ \sqrt{((x-x^')^2+(y-y^')^2}} + \sigma (x,y) ( 1 ) - elastic reaction of formation
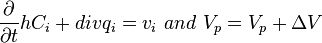\frac{\partial}{\partial t} h C_i + div q_i = v_i\ and\ V_p = V_p + \Delta V ( 2 ) - 2D equation of multifluid flow and proppant transport

The model accounts for the effect of proppant bridging and gravitational setting.

The mathematical model is supplemented by rheological dependencies for coupling the flow of a fluid with a pressure gradient and equations for calculating leaks into the reservoir.

Splitting by physical processes

In usual numerical Planar3D implementation, Jacobi matrix includes parts that describe geomechanical and hydrodynamical processes. Splitting by physical processes allows to solve geomechanics and hydrodynamics separately. Splitting turns one linear system with dense matrix into two. Separate solving requires significantly less computation resources than solving whole system.

References

  1. ↑ 1.0 1.1 Economides, Michael J.; Oligney, Ronald; Valko, Peter (2002). Unified Fracture Design: Bridging the Gap Between Theory and Practice. Alvin, Texas: Orsa Press. 

Pages in category "OnPlan"

The following 4 pages are in this category, out of 4 total.

H

O

Retrieved from "https://wiki.pengtools.com/index.php?title=Category:OnPlan&oldid=4872"