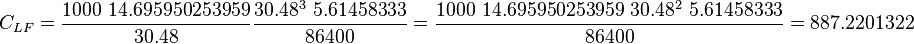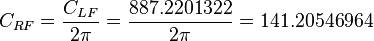Difference between revisions of "141.2 derivation"
From wiki.pengtools.com
(→Math and Physics) |
(→Math and Physics) |
||
| Line 24: | Line 24: | ||
And: | And: | ||
| − | :<math> \frac{[bbl]}{[day]} = - | + | :<math> \frac{[bbl]}{[day]} = - C_{LF} \frac{[mD][ft^2]}{[cP]} \frac{[psia]}{[ft]}</math> |
where | where | ||
| − | :<math> | + | :<math> C_{LF} = \frac{1000\ 14.695950253959}{30.48} \frac{30.48^3\ 5.61458333}{86400} = \frac{1000\ 14.695950253959\ 30.48^2\ 5.61458333}{86400} = 887.2201322</math> |
| + | |||
| + | For the radial flow: | ||
| + | |||
| + | :<math> C_{RF} = \frac{C_{LF}}{2\pi} = \frac{887.2201322}{2\pi} = 141.20546964</math> | ||
==See Also== | ==See Also== | ||
Revision as of 06:07, 21 April 2018
Derivation of the 141.2 constant
141.2 is the well know constant with is used for converting from the Darcy's law units to the field units
Math and Physics
Darcy's law:
In Darcy's units:
Converting to the filed units:
So:
And:
where
For the radial flow:
See Also
Darcy's law
18.41 derivation
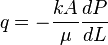
![\frac{[cm^3]}{[sec]} = - \frac{[D][cm^2]}{[cP]} \frac{[atm]}{[cm]}](/images/math/5/5/5/555b9dc7f65e6db7f1cd05153aaae770.png)
![\frac{[cm^3] \frac{[ft^3]}{[30.48^3 cm^3]} \frac{[bbl]}{[5.61458333 ft^3]} }{[sec] \frac{[day]}{[86400 sec]}} = - \frac{[D] \frac{[1000 mD]}{[D]}[cm^2] \frac{[ft^2]}{[30.48^2 cm]}}{[cP]} \frac{[atm] \frac{[14.695950253959 psia]}{[atm]}}{[cm] \frac{[ft]}{[30.48 cm]}}](/images/math/1/9/0/190503f228c14db727074159d40e455b.png)
![\frac{[bbl]}{[day]} \frac{86400}{30.48^3\ 5.61458333} = - \frac{[mD][ft^2]}{[cP]} \frac{[psia]}{[ft]} \frac{1000\ 14.695950253959}{30.48}](/images/math/9/a/b/9abe955d3e8338add13d1fe96e9fd738.png)
![\frac{[bbl]}{[day]} = - C_{LF} \frac{[mD][ft^2]}{[cP]} \frac{[psia]}{[ft]}](/images/math/d/d/4/dd4c5bbb71e5c38a6ae238f62d56d9ea.png)