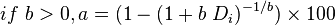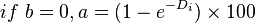Difference between revisions of "Decline Curve Analysis"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Nomenclature)
(→‎Math & Physics)
Line 23: Line 23:
 
<tr>
 
<tr>
 
<td>Exponential decline, b = 0</td>
 
<td>Exponential decline, b = 0</td>
−
<td><math>q(t) = {q_i}^{-D_i\ t}</math></td>
+
<td><math>q(t) = {q_i}\ e^{-D_i\ t}</math></td>
 
<td><math>Q = \frac{q_i-q(t)}{D_i}</math></td>
 
<td><math>Q = \frac{q_i-q(t)}{D_i}</math></td>
 
</tr>
 
</tr>

Revision as of 18:19, 27 October 2017

Brief

Decline Curve Analysis (DCA) is an empirical method for rate decline analysis and rate forecasting published by Arps in 1945 [1].

DCA is applied for Wells and Reservoirs production forecasting.

Math & Physics

Note Rate Cumulative
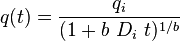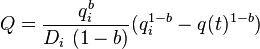Hyperbolic decline, 0 < b < 1 [2] q(t) = \frac{q_i}{(1+b\ D_i\ t)^{1/b}} Q = \frac{q^b_i}{D_i\ (1-b)} (q^{1-b}_i-q(t)^{1-b})
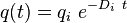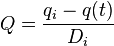Exponential decline, b = 0 q(t) = {q_i}\ e^{-D_i\ t} Q = \frac{q_i-q(t)}{D_i}
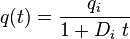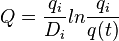Harmonic decline, b = 1 q(t) = \frac{q_i}{1+D_i\ t} Q = \frac{q_i}{D_i} ln{\frac{q_i}{q(t)}}

Discussion

If one has a need to convert decline factor Di to the actual annual decline in %:

if\ b > 0, a = (1 - (1 + b\ D_i)^{- 1 / b}) \times 100
if\ b = 0, a = (1 - e^{-D_i}) \times 100

Nomenclature

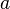a = annual decline, %
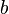b = decline curve parametr, dimensionless
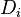D_i = decline factor per time t, dimensionless
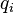q_i = initial rate, any rate units applies
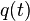q(t) = rate at time t, any rate units applies
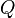Q = cumulatve rate at time t, any rate units applies
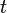t = forecast time, days

References

  1. ↑ Arps, J. J. (1945). "Analysis of Decline Curves"Paid subscription required. Transactions of the AIME. Society of Petroleum Engineers. 160 (01). 
  2. ↑ "KAPPA Dynamic Data Analysis (DDA) book"Paid subscription required. 
Retrieved from "https://wiki.pengtools.com/index.php?title=Decline_Curve_Analysis&oldid=2828"