Difference between revisions of "Decline Curve Analysis"
From wiki.pengtools.com
(→Math & Physics) |
|||
| Line 35: | Line 35: | ||
</table> | </table> | ||
| + | === Nomenclature === | ||
| + | :<math> A_1..A_{11} </math> = coefficients | ||
| + | :<math> \rho_r </math> = reduced density, dimensionless | ||
| + | :<math> P </math> = pressure, psia | ||
| + | :<math> P_{pc} </math> = pseudo critical pressure, psia | ||
| + | :<math> P_{pr} </math> = pseudoreduced pressure, dimensionless | ||
| + | :<math> SG_g </math> = gas specific gravity, dimensionless | ||
| + | :<math> T </math> = temperature, °R | ||
| + | :<math> T_{pc} </math> = pseudo critical temperature, °R | ||
| + | :<math> T_{pr} </math> = pseudoreduced temperature, dimensionless | ||
| + | :<math> z </math> = gas compressibility factor, dimensionless | ||
== References == | == References == | ||
Revision as of 15:44, 26 October 2017
Brief
Decline Curve Analysis DCA is an empirical method for rate decline analysis and rate forecasting published by Arps in 1945 [1].
DCA is applied for Wells and Reservoirs production forecasting.
Math & Physics
| Note | Rate | Cumulative |
|---|---|---|
| Hyperbolic decline, 0 < b < 1 [2] |  |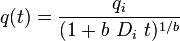
 |
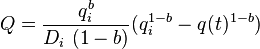| Exponential decline, b = 0 |  |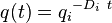
 |
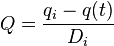| Harmonic decline, b = 1 |  |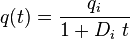
 |
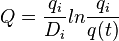Nomenclature
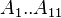= coefficients
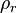= reduced density, dimensionless
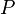= pressure, psia
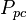= pseudo critical pressure, psia
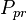= pseudoreduced pressure, dimensionless
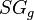= gas specific gravity, dimensionless
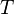= temperature, °R
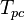= pseudo critical temperature, °R
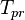= pseudoreduced temperature, dimensionless
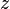= gas compressibility factor, dimensionless
References
- ↑ Arps, J. J. (1945). "Analysis of Decline Curves"
. Transactions of the AIME. Society of Petroleum Engineers. 160 (01).
- ↑ "KAPPA Dynamic Data Analysis (DDA) book".
