Difference between revisions of "Decline Curve Analysis"
From wiki.pengtools.com
(→Math & Physics) |
(→Math & Physics) |
||
| Line 16: | Line 16: | ||
<tr> | <tr> | ||
| − | <td> | + | <td>Hyperbolic decline, 0 < b < 1 <ref name = DDA/></td> |
<td><math>q(t) = \frac{q_i}{(1+b\ D_i\ t)^{1/b}}</math></td> | <td><math>q(t) = \frac{q_i}{(1+b\ D_i\ t)^{1/b}}</math></td> | ||
<td><math> Q = \frac{q^b_i}{D_i\ (1-b)} (q^{1-b}_i-q(t)^{1-b})</math></td> | <td><math> Q = \frac{q^b_i}{D_i\ (1-b)} (q^{1-b}_i-q(t)^{1-b})</math></td> | ||
| Line 24: | Line 24: | ||
<td>Exponential decline, b = 0</td> | <td>Exponential decline, b = 0</td> | ||
<td><math>q(t) = {q_i}^{-D_i\ t}</math></td> | <td><math>q(t) = {q_i}^{-D_i\ t}</math></td> | ||
| − | <td><math>q(t) = {q_i} | + | <td><math>Q = \frac{q_i-q(t)}{D_i}</math></td> |
| + | </tr> | ||
| + | |||
| + | <tr> | ||
| + | <td>Harmonic decline, b = 1</td> | ||
| + | <td><math>q(t) = \frac{q_i}{1+D_i\ t}</math></td> | ||
| + | <td><math>Q = \frac{q_i}{D_i} ln{\frac{q_i}{q(t)}}</math></td> | ||
</tr> | </tr> | ||
Revision as of 15:37, 26 October 2017
Contents
Brief
Decline Curve Analysis DCA is an empirical method for rate decline analysis and rate forecasting published by Arps in 1945 [1].
DCA is applied for Wells and Reservoirs production forecasting.
Math & Physics
| Note | Rate | Cumulative |
|---|---|---|
| Hyperbolic decline, 0 < b < 1 [2] |  |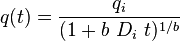
 |
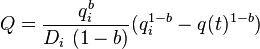| Exponential decline, b = 0 |  |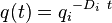
 |
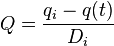| Harmonic decline, b = 1 |  |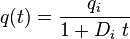
 |
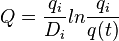References
- ↑ Arps, J. J. (1945). "Analysis of Decline Curves"
. Transactions of the AIME. Society of Petroleum Engineers. 160 (01).
- ↑ "KAPPA Dynamic Data Analysis (DDA) book".
