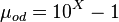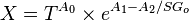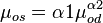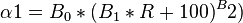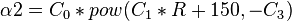Difference between revisions of "Beggs and Robinson Oil Viscosity correlation"
From wiki.pengtools.com
Gprotsykov (talk | contribs) (Created page with "__TOC__ === Brief === Beggs - Robinson correlation is ... === Math & Physics === Dead oil viscosity: :<math>\mu_{od} = 10^X-1</math><ref name= {Beggs - Robinson}/> w...") |
Gprotsykov (talk | contribs) |
||
| Line 24: | Line 24: | ||
where: | where: | ||
| + | |||
B0 = 10.715<br/> | B0 = 10.715<br/> | ||
B1 = 5.615<br/> | B1 = 5.615<br/> | ||
Revision as of 08:14, 14 June 2017
Contents
Brief
Beggs - Robinson correlation is ...
Math & Physics
Dead oil viscosity:
where:
A0 = -1.163
A1 = 13.108
A2 = 6.591
Saturated oil viscosity:
where:
B0 = 10.715
B1 = 5.615
B2 = 0.515
C0 = 5.44
C1 = 5.615
C2 = 0.338
Discussion
Workflow
Application range
Nomenclature
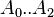= coefficients
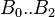= coefficients
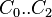= coefficients
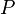= pressure, MPA
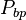= bubble point pressure, MPA
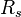= oil gas ration, m3/m3
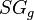= gas specific gravity, dimensionless
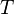= temperature, °R
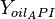= oil API gravity, dimensionless
References
- ↑
Vazquez, M.; Beggs, H.D. (1980). "Correlations for Fluid Physical Property Prediction."
. Society of Petroleum Engineers (SPE-6719-PA).
