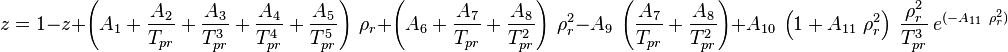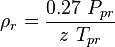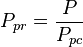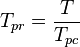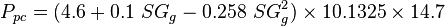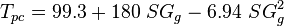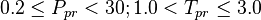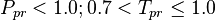Difference between revisions of "Dranchuk correlation"

Revision as of 07:29, 12 May 2017

z = 1-z+ \left(A_1 +\frac{A_2}{T_{pr}} +\frac{A_3}{T^3_{pr}} +\frac{A_4}{T^4_{pr}} +\frac{A_5}{T^5_{pr}} \right)\ \rho_r+ \left(A_6 +\frac{A_7}{T_{pr}} +\frac{A_8}{T^2_{pr}} \right)\ \rho^2_r -A_9\ \left(\frac{A_7}{T_{pr}}+\frac{A_8}{T^2_{pr}}\right) +A_{10}\ \left(1+A_{11}\ \rho^2_r\right)\ \frac{\rho^2_r}{T^3_{pr}} \ e^{(-A_{11}\ \rho^2_r)}

^[2]

where:

\rho_r = \frac{0.27\ P_{pr}}{{z\ T_{pr}}}

P_{pr} = \frac{P}{P_{pc}}

T_{pr} = \frac{T}{T_{pc}}

Why the Dranchuk correlation?

It's classics!
— www.pengtools.com

To solve the Dranchuk equation use the iterative secant method.

To find the pseudo critical properties from the gas specific gravity ^[1]:

P_{pc} = (4.6+0.1\ SG_g-0.258\ SG^2_g) \times 10.1325 \times 14.7

T_{pc} = 99.3+180\ SG_g-6.94\ SG^2_g

0.2 \le P_{pr} < 30 ; 1.0 < T_{pr} \le 3.0

^[2]

and

P_{pr} < 1.0 ; 0.7 < T_{pr} \le 1.0

^[2]

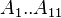A_1..A_{11}

= coefficients

\rho_r

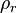= reduced density, dimensionless

P

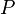= pressure, psia

P_{pc}

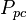= pseudo critical pressure, psia

P_{pr}

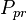= pseudoreduced pressure, dimensionless

SG_g

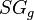= gas specific gravity, dimensionless

T

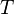= temperature, °R

T_{pc}

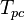= pseudo critical temperature, °R

T_{pr}

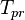= pseudoreduced temperature, dimensionless

z

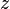= gas compressibility factor, dimensionless

↑ ^1.0 ^1.1 Standing, M. B.; Katz, D. L. (December 1942). "Density of Natural Gases". Transactions of the AIME. Society of Petroleum Engineers. 146 (SPE-942140-G).
↑ ^2.0 ^2.1 ^2.2 Dranchuk, P. M.; Abou-Kassem, H. (July 1975). "Calculation of Z Factors For Natural Gases Using Equations of State". The Journal of Canadian Petroleum. 14 (PETSOC-75-03-03).

@@ Line 52: / Line 52: @@
 To find the pseudo critical properties from the gas specific gravity <ref name=Standing&Katz />:
-:<math>  P_{pc} =  4.6+0.1\ SG_g-0.258\ SG^2_g</math>
+:<math>  P_{pc} =  (4.6+0.1\ SG_g-0.258\ SG^2_g) \times 10.1325 \times 14.7</math>
 :<math>  T_{pc} =  99.3+180\ SG_g-6.94\ SG^2_g</math>