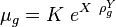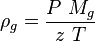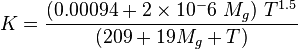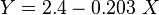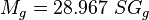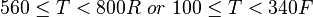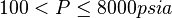Difference between revisions of "Lee correlation"
From wiki.pengtools.com
(→Math & Physics) |
(→Math & Physics) |
||
| Line 9: | Line 9: | ||
:<math> \mu_g = K\ e^{X\ \rho_g^Y} </math><ref name= Lee/> | :<math> \mu_g = K\ e^{X\ \rho_g^Y} </math><ref name= Lee/> | ||
where | where | ||
| − | :<math> \ | + | :<math> \rho_g = \frac{P\ M_g}{z\ T}</math> |
:<math> K = \frac{(0.00094+2\times10^-6\ M_g)\ T^{1.5}}{(209+19M_g+T)}</math> | :<math> K = \frac{(0.00094+2\times10^-6\ M_g)\ T^{1.5}}{(209+19M_g+T)}</math> | ||
Revision as of 14:18, 2 May 2017
Brief
Lee correlation for viscosity of natural gases.
Math & Physics
where
Discussion
Why the Lee correlation?
Application range
Nomenclature
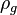= gas density, g/cm3
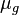= gas viscosity, cp
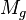= gas molecular weight
= pressure, psia
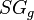= gas specific gravity, dimensionless
= temperature, °R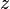
= gas compressibility factor, dimensionless
References
- ↑ Lee, A. B.; Gonzalez, M. H.; Eakin, B. E. (1966). "The Viscosity of Natural Gases". J Pet Technol (SPE-1340-PA).
