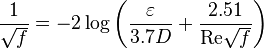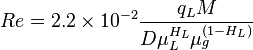Difference between revisions of "Gray correlation"
From wiki.pengtools.com
(→Math & Physics) |
(→Math & Physics) |
||
| Line 9: | Line 9: | ||
where | where | ||
| − | :<math> \rho_m | + | :<math> \rho_m </math> = No-slip mixture density |
Colebrook–White <ref name=Colebrook/> equation for the [http://en.wikipedia.org/wiki/Darcy_friction_factor_formulae Darcy's friction factor]: | Colebrook–White <ref name=Colebrook/> equation for the [http://en.wikipedia.org/wiki/Darcy_friction_factor_formulae Darcy's friction factor]: | ||
Revision as of 12:24, 4 April 2017
Brief
- The boundary between the bubble and slug flow[1]
Math & Physics
Following the law of conservation of energy the basic steady state flow equation is:
where
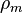 = No-slip mixture density
= No-slip mixture density
Colebrook–White [2] equation for the Darcy's friction factor:
Reynolds two phase number:
Discussion
Workflow
To find Hg calculate:
Nomenclature
References
- ↑ 1.0 1.1 Gray, H. E. (1974). "Vertical Flow Correlation in Gas Wells". User manual for API 14B, Subsurface controlled safety valve sizing computer program. API.
- ↑ Colebrook, C. F. (1938–1939). "Turbulent Flow in Pipes, With Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws"
 . Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
. Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
- ↑ Moody, L. F. (1944). "Friction factors for pipe flow"
 . Transactions of the ASME. 66 (8): 671–684.
. Transactions of the ASME. 66 (8): 671–684.
![144 \frac{\Delta p}{\Delta h} = [\rho_g H_g + \rho_L (1-H_g)] + \rho_m \frac{f v_m^2 }{2 g_c D} + \rho_m \frac{\Delta{(\frac{v_m^2}{2g_c}})}{\Delta h}](/images/math/4/a/2/4a29b6936a25231ffeecf44d6a3b7dd5.png)