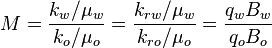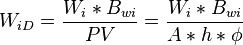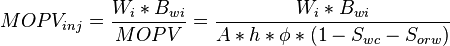Difference between revisions of "Mobility Ratio"
From wiki.pengtools.com
(→Equation) |
(→Equation) |
||
| Line 7: | Line 7: | ||
===Equation=== | ===Equation=== | ||
| − | :<math> M = \frac{k_w/ \mu_w}{k_o/ \mu_o}=\frac{k_{rw | + | :<math> M = \frac{k_w/ \mu_w}{k_o/ \mu_o}=\frac{k_{rw}/ \mu_w}{k_{ro}/ \mu_o}=\frac{q_w B_w}{q_o B_o}</math> |
where | where | ||
Revision as of 13:58, 25 March 2022
Brief
Mobility Ratio determines the relative rate of one fluid to another (etc. water to oil). The waterflood is driven by pore volumes of injected fluid. Everything that is of practical interest occurs between zero to three pore volumes injected [1].
Equation
where
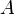= Area, m2
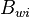= Injected water formation oil factor, m3/m3
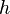= Net pay, oil saturated thickness, m
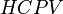= Hydrocarbon pore volume, m3
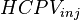= Injected hydrocarbon pore volumes, fraction
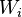= Cumulative water injection volume, m3
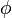= Porosity, fraction
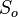= Oil saturation, fraction
Related definitions
Dimensionless injected pore volume:
Injected movable pore volume:
where
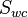= Connate water saturation, fraction
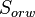= Residual oil saturation to water, fraction
See Also
References
- ↑
Wolcott, Don (2009). Applied Waterflood Field Development
. Houston: Energy Tribune Publishing Inc.
