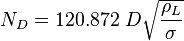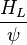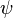Difference between revisions of "Hagedorn and Brown correlation"
From wiki.pengtools.com
| Line 18: | Line 18: | ||
Reynolds two phase number: | Reynolds two phase number: | ||
:<math> Re = 2.2 \times 10^{-2} \frac {q_L M}{D \mu_L^{H_L} \mu_g^{(1-H_L)}}</math> | :<math> Re = 2.2 \times 10^{-2} \frac {q_L M}{D \mu_L^{H_L} \mu_g^{(1-H_L)}}</math> | ||
| + | |||
| + | == Discussion == | ||
== Block Diagram == | == Block Diagram == | ||
Revision as of 16:38, 20 March 2017
Contents
Brief
Hagedorn and Brown is an empirical two-phase flow correlation published in 1965.
It doesn't distinguish between the flow regimes.
The heart of the Hagedorn and Brown method is a correlation for the liquid holdup :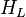 .
.
Math & Physics
Following the law of conservation of energy the basic steady state flow equation is:
where
Colebrook–White equation for the Darcy's friction factor:
Reynolds two phase number:
Discussion
Block Diagram
Workflow
corr p1
corr p2
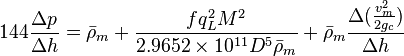
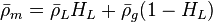
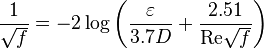
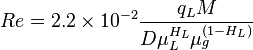
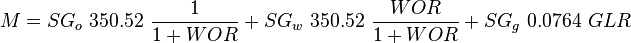
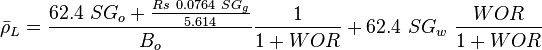
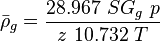
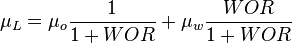
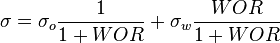
![N_L = 0.15726\ \mu_L \sqrt[4]{\frac{1}{\rho_L \sigma_L^3}}](/images/math/b/2/0/b207fe79b4a4ee53d466e182791ca737.png)
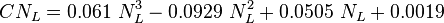
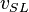
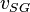
![N_{LV} = 1.938\ v_{SL}\ \sqrt[4]{\frac{\rho_L}{\sigma}}](/images/math/2/f/2/2f2abb2b5e504663beb5ddb87301af09.png)
![N_{GV} = 1.938\ v_{SG}\ \sqrt[4]{\frac{\rho_L}{\sigma}}](/images/math/4/0/c/40cab20a6f3a6a92f320bbff38c696cd.png)