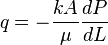Difference between revisions of "Darcy's law"
From wiki.pengtools.com
(→Darcy's law History) |
|||
| Line 13: | Line 13: | ||
By flowing water through the sand pack Darcy established that, for any flow rate, the velocity of the flow was directly proportional to the difference in manometric heights<ref name=DakeF/>: | By flowing water through the sand pack Darcy established that, for any flow rate, the velocity of the flow was directly proportional to the difference in manometric heights<ref name=DakeF/>: | ||
| − | [[File:Darcy's experimental equipment.png|300px| Darcy's experimental equipment]] | + | [[File:Darcy's experimental equipment.png|thumb|right|300px| Darcy's experimental equipment]] |
[[File:Les Fontaines Publiques de la Ville de Dijon.png|200px |link=https://books.google.ru/books?id=-FxYAAAAYAAJ&printsec=frontcover&hl=ru&source=gbs_ge_summary_r&cad=0#v=twopage&q&f=false]] | [[File:Les Fontaines Publiques de la Ville de Dijon.png|200px |link=https://books.google.ru/books?id=-FxYAAAAYAAJ&printsec=frontcover&hl=ru&source=gbs_ge_summary_r&cad=0#v=twopage&q&f=false]] | ||
Revision as of 13:55, 22 July 2019
Contents
Darcy's law
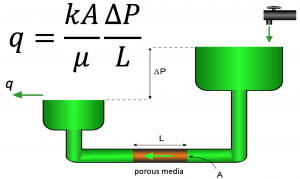
Darcy's law is the fundamental law of fluid motion in porous media published by Henry Darcy in 1856 [1].
Darcy's law has been successfully applied to determine the flow through permeable media since the early days of Petroleum Engineering.
Darcy's law History
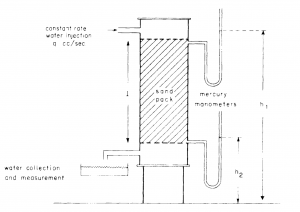
Henry Darcy worked on the design of a filter large enough to process the Dijon towns daily water requirement [2].
By flowing water through the sand pack Darcy established that, for any flow rate, the velocity of the flow was directly proportional to the difference in manometric heights[2]:
Darcy's law Equation
Conditions
- Single fluid
- Steady stay flow
- Constant fluid compressibility
- Constant temperature
Inflow Equations Derivation
Derivation of the Linear and Radial Inflow Equations
Nomenclature
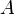= cross-sectional area, cm2
= permeability, d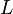
= length, cm
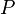= pressure, atm
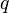= flow rate, cm3/sec
Greek symbols
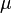= Darcy's law fluid viscosity, cp
See Also
Darcy's law application in Petroleum Engineering Technology.
References
- ↑ Darcy, Henry (1856). "Les Fontaines Publiques de la Ville de Dijon". Paris: Victor Dalmont.
- ↑ 2.0 2.1 Dake, L.P. (1978). Fundamentals of Reservoir Engineering. Amsterdam, Hetherlands: Elsevier Science. ISBN 0-444-41830-X.
