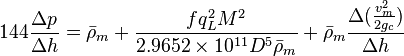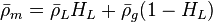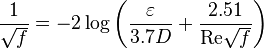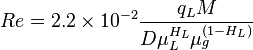Difference between revisions of "Hagedorn and Brown correlation"
From wiki.pengtools.com
(→Math & Physics) |
(→Math & Physics) |
||
| Line 17: | Line 17: | ||
Reynolds two phase number: | Reynolds two phase number: | ||
| − | :<math> Re = 2.2 \times 10^{-2} \frac {q_L M}{D \ | + | :<math> Re = 2.2 \times 10^{-2} \frac {q_L M}{D \mu_L^{H_L} \mu_g^{(1-H_L)}}</math> |
== Workflow == | == Workflow == | ||
Revision as of 08:06, 15 March 2017
Info
Hagedorn and Brown is an empirical two-phase flow correlation published in 1965.
It doesn't distinguish between the flow regimes.
The heart of the Hagedorn and Brown method is a correlation for the liquid holdup :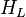 .
.
Math & Physics
The basic steady state flow equation is:
where
friction factor the Colebrook–White equation:
Reynolds two phase number:
Workflow
For each pipe segment find: