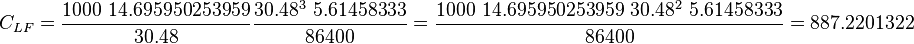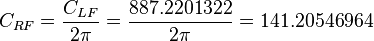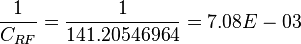Difference between revisions of "141.2 derivation"
From wiki.pengtools.com
(→Brief) |
(→Brief) |
||
| Line 1: | Line 1: | ||
== Brief== | == Brief== | ||
| − | '''141.2''' is the well know constant which is used for converting from the Darcy's law units to the field units in well's inflow equations: | + | '''141.2''' is the well know constant which is used for converting from the Darcy's law units to the field units in the well's inflow equations: |
:<math> q = \frac{1}{141.2} \frac{kh}{B\mu} \Delta P\ J_D = 7.08 \times 10^-3\ \frac{kh}{B\mu} \Delta P\ J_D</math> | :<math> q = \frac{1}{141.2} \frac{kh}{B\mu} \Delta P\ J_D = 7.08 \times 10^-3\ \frac{kh}{B\mu} \Delta P\ J_D</math> | ||
Revision as of 05:46, 23 April 2018
Brief
141.2 is the well know constant which is used for converting from the Darcy's law units to the field units in the well's inflow equations:
The derivation of the 141.2 constant is given below.
Math and Physics
Darcy's law:
In Darcy's units:
Converting to the field units:
So:
And:
where
For the radial flow:
One can be familiar with the inverse of the 141.2 constant:
See Also
Darcy's law
18.41 derivation
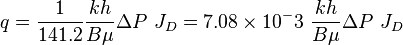
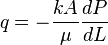
![\frac{[cm^3]}{[sec]} = - \frac{[D][cm^2]}{[cP]} \frac{[atm]}{[cm]}](/images/math/5/5/5/555b9dc7f65e6db7f1cd05153aaae770.png)
![\frac{[cm^3] \frac{[ft^3]}{[30.48^3 cm^3]} \frac{[bbl]}{[5.61458333 ft^3]} }{[sec] \frac{[day]}{[86400 sec]}} = - \frac{[D] \frac{[1000 mD]}{[D]}[cm^2] \frac{[ft^2]}{[30.48^2 cm]}}{[cP]} \frac{[atm] \frac{[14.695950253959 psia]}{[atm]}}{[cm] \frac{[ft]}{[30.48 cm]}}](/images/math/1/9/0/190503f228c14db727074159d40e455b.png)
![\frac{[bbl]}{[day]} \frac{86400}{30.48^3\ 5.61458333} = - \frac{[mD][ft^2]}{[cP]} \frac{[psia]}{[ft]} \frac{1000\ 14.695950253959}{30.48}](/images/math/9/a/b/9abe955d3e8338add13d1fe96e9fd738.png)
![\frac{[bbl]}{[day]} = - C_{LF} \frac{[mD][ft^2]}{[cP]} \frac{[psia]}{[ft]}](/images/math/d/d/4/dd4c5bbb71e5c38a6ae238f62d56d9ea.png)