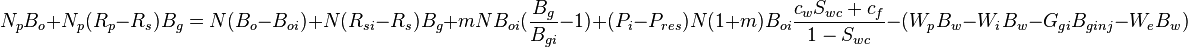Difference between revisions of "Oil Material Balance"
From wiki.pengtools.com
(→Nomenclature) |
(→Math & Physics) |
||
| Line 6: | Line 6: | ||
Equating all underground withdrawals to the sum of the volume changes<ref name=DakeF />: | Equating all underground withdrawals to the sum of the volume changes<ref name=DakeF />: | ||
| − | :<math>N_p B_o + N_p (R_p - R_s) B_g = N (B_o - B_{oi}) + N (R_{si} - R_s) B_g + m N B_{oi} (\frac{B_g}{B_{gi}} - 1) + (P_i - P_{res}) N (1 + m) B_{oi} \frac{c_w S_{wc} + c_f}{1 - | + | :<math>N_p B_o + N_p (R_p - R_s) B_g = N (B_o - B_{oi}) + N (R_{si} - R_s) B_g + m N B_{oi} (\frac{B_g}{B_{gi}} - 1) + (P_i - P_{res}) N (1 + m) B_{oi} \frac{c_w S_{wc} + c_f}{1 - S_{wc}}- (W_p B_w - W_i B_w - G_{gi} B_{ginj} - W_e B_w) </math> |
For use in the code to find Pres: | For use in the code to find Pres: | ||
Revision as of 13:11, 28 March 2018
Brief
The general form of the Oil Material Balance equation was first published by Schilthuis in 1941[1].
Math & Physics
Equating all underground withdrawals to the sum of the volume changes[1]:
For use in the code to find Pres:
Pres = Pi - (Np * Bo + Np * (Rp - Rs) * Bg + (Wp * Bw - Wi * Bw - Ggi * Bginj - We * Bw) - (N * (Bo - Boi) + N * (Rsi - Rs) * Bg + m * N * Boi * (Bg / Bgi - 1))) * (1 - Swc) / (N * (1 + m) * Boi * (cw * Swc + cf))
For use in the code to find Np:
Np = (N * (Bo - Boi) + N * (Rsi - Rs) * Bg + m * N * Boi * (Bg / Bgi - 1) + N * (1 + m) * Boi * (Pi - Pres) * (cw * Swc + cf) / (1 - Swc) - (Wp * Bw - Wi * Bw - Gging * Bgi - We * Bw)) / (Bo + (Rp - Rs) * Bg)
Discussion
... most powerful tool for investigating reservoirs and understanding their performance ...— L.P. Dake [2]
... the safest technique in the business since it's minimum assumption route through the subject of reservoir engineering ...— L.P. Dake [2]
See also
Nomenclature
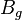= gas formation volume factor at Pres, bbl/scf
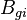= initial gas formation volume factor, bbl/scf
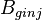= injection gas formation volume factor at Pres, bbl/scf
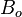= oil formation volume factor at Pres, bbl/stb
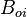= initial oil formation volume factor, bbl/stb
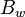= water formation volume factor at Pres, bbl/stb
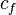= formation compressibility at initial pressure and temperature, 1/psia
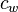= water compressibility at Pres, 1/psia
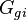= gas injection volume, scf
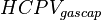= gas cap hydrocarbon pore volume, bbl
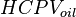= oil hydrocarbon pore volume, bbl
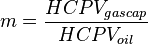, initial gas cap oil leg ratio, dimensionless
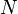= stock tank oil initially in place, stb
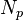= oil cumulative production volume, stb
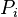= initial reservoir pressure, psia
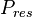= average reservoir pressure, psia
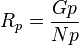, cumulative GOR, scf/stb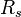
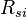= initial solution oil-gas ratio, scf/bbl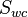
Swc
W_e
W_i
W_p
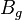= gas formation volume factor, ft3/scf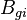- = initial gas formation volume factor, ft3/scf
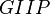= gas initially in place, scf
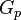= cumulative gas produced, scf
References
- ↑ 1.0 1.1 Dake, L.P. (1978). Fundamentals of Reservoir Engineering. Amsterdam, Hetherlands: Elsevier Science. ISBN 0-444-41830-X.
- ↑ 2.0 2.1 Dake, L.P. (1994). The Practice of Reservoir Engineering. Amsterdam, Hetherlands: Elsevier Science. ISBN 0-444-88538-2.
