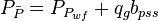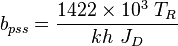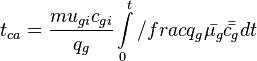Difference between revisions of "Gas Flowing Material Balance"
From wiki.pengtools.com
(→Math & Physics) |
(→Math & Physics) |
||
| Line 10: | Line 10: | ||
Combining the gas pseudo state flow equation and the [[Gas Material Balance]] equation: | Combining the gas pseudo state flow equation and the [[Gas Material Balance]] equation: | ||
| − | :<math> P_{\bar{P}}= P_{P_{wf}} + | + | :<math> P_{\bar{P}}= P_{P_{wf}} + q_g b_{pss}</math> <ref name=Mattar2005/> |
where | where | ||
:<math> b_{pss} = \frac{1422 \times 10^3\ T_R}{kh\ J_D}</math> | :<math> b_{pss} = \frac{1422 \times 10^3\ T_R}{kh\ J_D}</math> | ||
| + | |||
| + | Material balance pseudo-time: | ||
| + | |||
| + | :<math> t_{ca} = \frac{mu_{gi} c_{gi}}{q_g}\int\limits_{0}^{t}/frac{q_g}{\bar{\mu_g} \bar{\bar{c_g}}}dt</math> | ||
== References == | == References == | ||
Revision as of 12:29, 24 November 2017
Contents
Brief
Gas Flowing Material Balance is the advanced engineering technique to determine the Reservoirs GIIP and recovery as well as Well's EUR and JD.
Gas Flowing Material Balance is applied on the Well level given readily available well flowing data: production rate and tubing head pressure.
Math & Physics
Combining the gas pseudo state flow equation and the Gas Material Balance equation:
where
Material balance pseudo-time:
References
- ↑ Mattar, L.; Anderson, D (2005). "Dynamic Material Balance (Oil or Gas-In-Place Without Shut-Ins)" (PDF). CIPC.