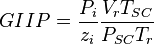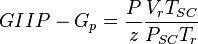Difference between revisions of "P/Z plot"

Revision as of 09:11, 21 November 2017

Brief

The P/Z plot is a plot of P/z versus cumulative gas production, G_p.

The interpretation technique is fitting the data points with the straight line to estimate GIIP.

The P/Z plot is based on the Gas Material Balance equation.

Math & Physics

Applying Real Gas EOS at reservoir conditions:

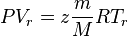PV_r=z\frac{m}{M} RT_r

(1)

Applying Real Gas EOS at standard conditions:

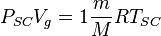P_{SC}V_g=1\frac{m}{M} RT_{SC}

(2)

Dividing eq. 2 by eq. 1 and rearranging:

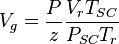V_g=\frac{P}{z} \frac{V_rT_{SC}}{P_{SC}T_{r}}

(3)

Applying eq. 3 for initial conditions and for any point in time:

GIIP=\frac{P_i}{z_i} \frac{V_rT_{SC}}{P_{SC}T_{r}}

Applying eq. 3 for any point in time:

GIIP-G_p=\frac{P}{z} \frac{V_rT_{SC}}{P_{SC}T_{r}}

Therefore at any time:

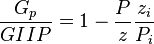\frac{G_p}{GIIP}=1-\frac{P}{z} \frac{z_i}{P_i}

, or

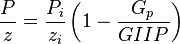
\frac{P}{z}=\frac{P_i}{z_i} \left (1- \frac{G_p}{GIIP}\right )

Thus a plot of P/z vs cumulative produced gas is a straight line intersecting X axis at GIIP.

Discussion

Griffith correlation adds a hook to the originally straight Hagedorn and Brown VLP curve.

Nomenclature

GIIP

= gas initially in place, ft³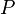

P

= reservoir pressure (changing), psia

P_{SC}

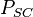= pressure at standard conditions, psia

P_{i}

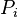= initial reservoir pressure, psia

z

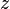= gas compressibility factor, dimensionless

T_r

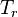= reservoir pressure (constant), °R

T_{SC}

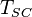= temperature at standard conditions, °R

T_i

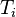= initial reservoir pressure, °R

V_r

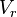= reservoir volume (constant), ft³

V_g

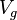= volume of gas in reservoir converted to standard conditions (changing), ft³

References

Cite error: <ref> tag defined in <references> has group attribute "" which does not appear in prior text.
Cite error: <ref> tag defined in <references> has group attribute "" which does not appear in prior text.
Cite error: <ref> tag defined in <references> has group attribute "" which does not appear in prior text.

@@ Line 35: / Line 35: @@
 == Nomenclature  ==
-:<math> D </math> = pipe diameter, ft
+:<math> GIIP </math> = gas initially in place, ft<sup>3</sup>
-:<math> H_g </math> = gas holdup factor, dimensionless
+:<math> P </math> = reservoir pressure (changing), psia
-:<math> L_B </math> = bubble-slug boundary, dimensionless
+:<math> P_{SC} </math> = pressure at standard conditions, psia
-:<math> v_g </math> = gas velocity, ft/sec
+:<math> P_{i} </math> = initial reservoir pressure, psia
-:<math> v_L </math> = liquid velocity, ft/sec
+:<math> z </math> = gas compressibility factor, dimensionless
-:<math> v_s </math> = 0.8, slip velocity (difference between average gas and liquid velocities), ft/sec
+:<math> T_r </math> = reservoir pressure (constant), °R
+:<math> T_{SC} </math> = temperature at standard conditions, °R
+:<math> T_i </math> = initial reservoir pressure, °R
+:<math> V_r </math> = reservoir volume (constant), ft<sup>3</sup>
+:<math> V_g </math> = volume of gas in reservoir converted to standard conditions (changing), ft<sup>3</sup>
 == References ==

Navigation menu

Navigation

Categories

Products