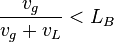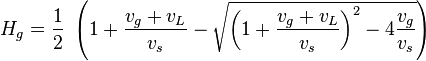Difference between revisions of "Griffith correlation"
From wiki.pengtools.com
(→Subscripts) |
(→Nomenclature) |
||
| Line 20: | Line 20: | ||
:<math> H_g </math> = gas holdup factor, dimensionless | :<math> H_g </math> = gas holdup factor, dimensionless | ||
:<math> L_B </math> = bubble-slug boundary, dimensionless | :<math> L_B </math> = bubble-slug boundary, dimensionless | ||
| − | :<math> | + | :<math> v_g </math> = gas velocity, ft/sec |
| + | :<math> v_L </math> = liquid velocity, ft/sec | ||
:<math> v_s </math> = 0.8, slip velocity (difference between average gas and liquid velocities), ft/sec | :<math> v_s </math> = 0.8, slip velocity (difference between average gas and liquid velocities), ft/sec | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== References == | == References == | ||
Revision as of 16:59, 27 March 2017
Brief
The Griffith correlation [1] is an empirical correlation which defines:
- The boundary between the bubble and slug flow[2]
- The void fraction of gas in bubble flow - gas hold up Hg[2]
Math & Physics
The bubble flow exist when:
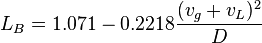, with the limit 
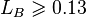[2]
The gas holdup:
Discussion
Nomenclature
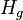= gas holdup factor, dimensionless
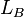= bubble-slug boundary, dimensionless
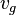= gas velocity, ft/sec
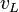= liquid velocity, ft/sec
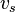= 0.8, slip velocity (difference between average gas and liquid velocities), ft/sec
References
- ↑ Griffith, P.; Wallis, G. B. (August 1961). "Two-Phase Slug Flow"
. Journal of Heat Transfer. ASME. 83: 307–320.
- ↑ 2.0 2.1 2.2 2.3 Orkiszewski, J. (June 1967). "Predicting Two-Phase Pressure Drops in Vertical Pipe". Journal of Petroleum Technology. SPE. 19 (SPE-1546-PA).
- ↑ Economides, M.J.; Hill, A.D.; Economides, C.E.; Zhu, D. (2013). Petroleum Production Systems (2 ed.). Westford, Massachusetts: Prentice Hall. ISBN 978-0-13-703158-0.
