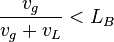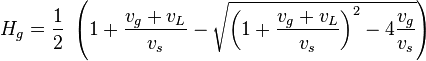Difference between revisions of "Griffith correlation"
From wiki.pengtools.com
(→Math & Physics) |
(→Nomenclature) |
||
| Line 21: | Line 21: | ||
:<math> f </math> = friction factor, dimensionless | :<math> f </math> = friction factor, dimensionless | ||
:<math> GLR </math> = gas-liquid ratio, scf/bbl | :<math> GLR </math> = gas-liquid ratio, scf/bbl | ||
| + | :<math> L_B </math> = bubble-slug boundary, dimensionless | ||
:<math> M </math> = total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lb<sub>m</sub>/bbl | :<math> M </math> = total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lb<sub>m</sub>/bbl | ||
:<math> N_D </math> = pipe diameter number number, dimensionless | :<math> N_D </math> = pipe diameter number number, dimensionless | ||
Revision as of 16:55, 27 March 2017
Brief
The Griffith correlation [1] is an empirical correlation which defines:
- The boundary between the bubble and slug flow[2]
- The void fraction of gas in bubble flow - gas hold up Hg[2]
Math & Physics
The bubble flow exist when:
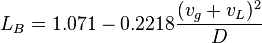, with the limit 
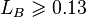[2]
The gas holdup:
Discussion
Nomenclature
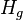= gas holdup factor, dimensionless
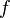= friction factor, dimensionless
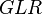= gas-liquid ratio, scf/bbl
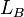= bubble-slug boundary, dimensionless
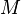= total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl
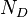= pipe diameter number number, dimensionless
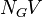= gas velocity number, dimensionless
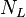= liquid viscosity number, dimensionless
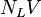= liquid velocity number, dimensionless
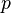= pressure, psia
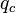= conversion constant equal to 32.174, lbmft / lbfsec2
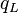= total liquid production rate, bbl/d
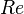= Reynolds number, dimensionless
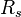= solution gas-oil ratio, scf/stb
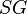= specific gravity, dimensionless
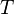= temperature, °R or °K, follow the subscript
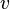= velocity, ft/sec
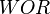= water-oil ratio, bbl/bbl
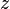= gas compressibility factor, dimensionless
References
- ↑ Griffith, P.; Wallis, G. B. (August 1961). "Two-Phase Slug Flow"
. Journal of Heat Transfer. ASME. 83: 307–320.
- ↑ 2.0 2.1 2.2 2.3 Orkiszewski, J. (June 1967). "Predicting Two-Phase Pressure Drops in Vertical Pipe". Journal of Petroleum Technology. SPE. 19 (SPE-1546-PA).
- ↑ Economides, M.J.; Hill, A.D.; Economides, C.E.; Zhu, D. (2013). Petroleum Production Systems (2 ed.). Westford, Massachusetts: Prentice Hall. ISBN 978-0-13-703158-0.
