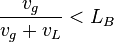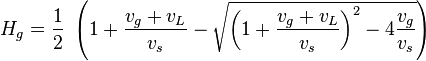Difference between revisions of "Griffith correlation"

From wiki.pengtools.com
Jump to: navigation, search
(→‎References)
(→‎Math & Physics)
Line 8: Line 8:
  
 
The bubble flow exist when:
 
The bubble flow exist when:
−
:<math> \frac{v_g}{v_g + v_L} < L_B </math><ref name= Orkiszewski />
+
:<math> \frac{v_g}{v_g + v_L} < L_B </math><ref name= Economides />
  
 
:<math> L_B = 1.071 - 0.2218 \frac{(v_g+v_L)^2}{D}</math>, with the limit <math> L_B \geqslant 0.13 </math><ref name= Orkiszewski />
 
:<math> L_B = 1.071 - 0.2218 \frac{(v_g+v_L)^2}{D}</math>, with the limit <math> L_B \geqslant 0.13 </math><ref name= Orkiszewski />

Revision as of 16:54, 27 March 2017

Brief

The Griffith correlation [1] is an empirical correlation which defines:

  • The boundary between the bubble and slug flow[2]
  • The void fraction of gas in bubble flow - gas hold up Hg[2]

Math & Physics

The bubble flow exist when:

\frac{v_g}{v_g + v_L} < L_B [3]
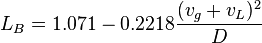L_B = 1.071 - 0.2218 \frac{(v_g+v_L)^2}{D}, with the limit 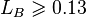L_B \geqslant 0.13 [2]

The gas holdup:

H_g = \frac{1}{2}\ \left ( 1 + \frac{v_g+v_L}{v_s} - \sqrt{ \left ( 1 + \frac{v_g+v_L}{v_s} \right )^2 - 4 \frac{v_g}{v_s}} \right ) [2]

Discussion

Nomenclature

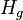H_g = gas holdup factor, dimensionless
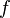f = friction factor, dimensionless
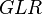GLR = gas-liquid ratio, scf/bbl
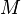M = total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lbm/bbl
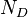N_D = pipe diameter number number, dimensionless
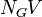N_GV = gas velocity number, dimensionless
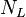N_L = liquid viscosity number, dimensionless
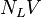N_LV = liquid velocity number, dimensionless
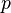p = pressure, psia
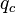q_c = conversion constant equal to 32.174, lbmft / lbfsec2
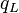q_L = total liquid production rate, bbl/d
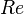Re = Reynolds number, dimensionless
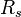R_s = solution gas-oil ratio, scf/stb
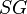SG = specific gravity, dimensionless
T = temperature, °R or °K, follow the subscript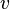
v = velocity, ft/sec
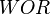WOR = water-oil ratio, bbl/bbl
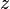z = gas compressibility factor, dimensionless

References

  1. ↑ Griffith, P.; Wallis, G. B. (August 1961). "Two-Phase Slug Flow"Paid subscription required. Journal of Heat Transfer. ASME. 83: 307–320. 
  2. ↑ 2.0 2.1 2.2 2.3 Orkiszewski, J. (June 1967). "Predicting Two-Phase Pressure Drops in Vertical Pipe"Paid subscription required. Journal of Petroleum Technology. SPE. 19 (SPE-1546-PA). 
  3. ↑ Economides, M.J.; Hill, A.D.; Economides, C.E.; Zhu, D. (2013). Petroleum Production Systems (2 ed.). Westford, Massachusetts: Prentice Hall. ISBN 978-0-13-703158-0. 
Retrieved from "https://wiki.pengtools.com/index.php?title=Griffith_correlation&oldid=1787"