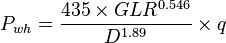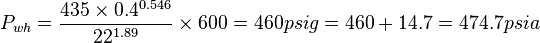Difference between revisions of "Gilbert choke equation"
From wiki.pengtools.com
(→Brief) |
(→Brief) |
||
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <div style='text-align: right;'>By Mikhail Tuzovskiy on {{REVISIONTIMESTAMP}}</div> | ||
__TOC__ | __TOC__ | ||
==Brief== | ==Brief== | ||
| − | The most common formula used for multiphase flow through surface chokes by Gilbert <ref name=Gilbert | + | The most common formula used for multiphase flow through surface chokes developed by '''Gilbert''' in 1954<ref name=Gilbert/>. |
| − | Gilbert developed his empirical equation from field data in California. | + | Gilbert developed his empirical equation from field data in California<ref name=KermitBrown1984/>. |
==Math and Physics== | ==Math and Physics== | ||
:<math>P_{wh}=\frac{435 \times GLR^{0.546}}{D^{1.89}} \times q</math> | :<math>P_{wh}=\frac{435 \times GLR^{0.546}}{D^{1.89}} \times q</math> | ||
| − | Note that the equation is independent of the downstream pressure and assumes that the downstream pressure is less than 70% of the upstream pressure, i.e. the flow is "critical" | + | Note that the equation is independent of the downstream pressure and assumes that the downstream pressure is less than 70% of the upstream pressure, i.e. the flow is "critical" i.e. fluid reach sonic velocity in the throat of the choke<ref name=Economides/>. |
==Example== | ==Example== | ||
===Given data=== | ===Given data=== | ||
| − | Oil rate = 600 bbl/d, GLR=400 scf/bbl, D=22/64 in, Line pressure = 180 | + | Oil rate = 600 bbl/d, GLR=400 scf/bbl, D=22/64 in, Line pressure = 180 psia |
Calculate the well head pressure? | Calculate the well head pressure? | ||
===Solution=== | ===Solution=== | ||
| − | :<math>P_{wh}=\frac{435 \times 0.4^{0.546}}{22^{1.89}} \times 600 = 460 | + | :<math>P_{wh}=\frac{435 \times 0.4^{0.546}}{22^{1.89}} \times 600 = 460 psig = 460 +14.7 = 474.7 psia</math> |
| − | Validity check 180/ | + | Validity check 180/474.7=0.38 < 0.7 OK |
==Nomenclature== | ==Nomenclature== | ||
:<math>D</math> = choke beam diametr, 64th of an inch | :<math>D</math> = choke beam diametr, 64th of an inch | ||
:<math>GLR</math> = gas liquid ratio, Mscf/bbl or 10^3 scf/bbl | :<math>GLR</math> = gas liquid ratio, Mscf/bbl or 10^3 scf/bbl | ||
| − | :<math>P_{wh}</math> = well head pressure, | + | :<math>P_{wh}</math> = well head pressure, psig |
| − | :<math>q</math> = flow rate, bbl/d | + | :<math>q</math> = liquid flow rate, bbl/d |
== References == | == References == | ||
| Line 43: | Line 44: | ||
|place=Tulsa, Oklahoma | |place=Tulsa, Oklahoma | ||
}}</ref> | }}</ref> | ||
| − | + | <ref name=Economides>{{cite book | |
| + | |last1= Economides |first1=M.J. | ||
| + | |last2= Hill |first2=A.D. | ||
| + | |last3= Economides |first3=C.E. | ||
| + | |last4= Zhu |first4=D. | ||
| + | |title=Petroleum Production Systems | ||
| + | |edition=2 | ||
| + | |date=2013 | ||
| + | |publisher=Prentice Hall | ||
| + | |place=Westford, Massachusetts | ||
| + | |isbn=978-0-13-703158-0 | ||
| + | }}</ref> | ||
</references> | </references> | ||
Latest revision as of 19:10, 8 November 2024
By Mikhail Tuzovskiy on 20241108191031
Contents
Brief
The most common formula used for multiphase flow through surface chokes developed by Gilbert in 1954[1].
Gilbert developed his empirical equation from field data in California[2].
Math and Physics
Note that the equation is independent of the downstream pressure and assumes that the downstream pressure is less than 70% of the upstream pressure, i.e. the flow is "critical" i.e. fluid reach sonic velocity in the throat of the choke[3].
Example
Given data
Oil rate = 600 bbl/d, GLR=400 scf/bbl, D=22/64 in, Line pressure = 180 psia
Calculate the well head pressure?
Solution
Validity check 180/474.7=0.38 < 0.7 OK
Nomenclature
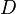= choke beam diametr, 64th of an inch
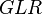= gas liquid ratio, Mscf/bbl or 10^3 scf/bbl
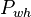= well head pressure, psig
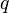= liquid flow rate, bbl/d
References
- ↑ Gilbert, W.E. (1954). Flowing and Gas-Lift Well Performance. Drilling and Production Practice API. p. 143.
- ↑ Brown, Kermit (1984). The Technology of Artificial Lift Methods. Volume 4. Production Optimization of Oil and Gas Wells by Nodal System Analysis. Tulsa, Oklahoma: PennWellBookss.
- ↑ Economides, M.J.; Hill, A.D.; Economides, C.E.; Zhu, D. (2013). Petroleum Production Systems (2 ed.). Westford, Massachusetts: Prentice Hall. ISBN 978-0-13-703158-0.
