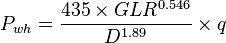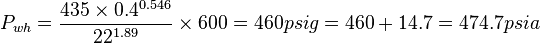Difference between revisions of "Gilbert choke equation"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Math and Physics)
(→‎Brief)
 
(33 intermediate revisions by the same user not shown)
Line 1: Line 1:
 +
<div style='text-align: right;'>By Mikhail Tuzovskiy on {{REVISIONTIMESTAMP}}</div>
 
__TOC__
 
__TOC__
 
==Brief==
 
==Brief==
−
The most common used formula for multiphase flow through surface chokes by Gilbert <ref name=KermitBrown1984/>.
+
The most common formula used for multiphase flow through surface chokes developed by '''Gilbert''' in 1954<ref name=Gilbert/>.
  
−
Echometer is used to measure the fluid level in the wells.
+
Gilbert developed his empirical equation from field data in California<ref name=KermitBrown1984/>.
  
−
Fluid level is used to calculate and monitor the bottom hole pressure of the wells.
+
==Math and Physics==
 +
:<math>P_{wh}=\frac{435 \times GLR^{0.546}}{D^{1.89}} \times q</math>
  
−
==Math and Physics==
+
Note that the equation is independent of the downstream pressure and assumes that the downstream pressure is less than 70% of the upstream pressure, i.e. the flow is "critical" i.e. fluid reach sonic velocity in the throat of the choke<ref name=Economides/>.
−
:<math>P_{wh}=\frac{435\ GLR^0.546}{D^1.89}\q</math>
+
 
 +
==Example==
 +
===Given data===
 +
Oil rate = 600 bbl/d, GLR=400 scf/bbl, D=22/64 in, Line pressure = 180 psia
  
−
===Flowing well fluids segregation===
+
Calculate the well head pressure?
−
When the well is flowing with the pump this is how fluids segregate in the well bore:
 
−
*Oil, gas and water are produced through the tubing from the reservoir to the surface 
 
−
*Gas is in the annulus from the surface to the fluid level, Hd
 
−
*Oil and gas are between the fluid level Hd, and the pump setting depth, Hd
 
−
*Water, oil and gas are between pump, Hd and the top of the perforations, Hperfs
 
−
*Water is in the rathole
 
  
−
===Equation to calculate the BHP from the fluid level===
+
===Solution===
−
:<math>P_{wf}=P_{ann}+\frac{(H_{perfs}-H_{pump})(SG_o(1-WCUT)+SG_w WCUT)+(H_{pump}-H_d)SG_o}{10.32}</math>
+
:<math>P_{wh}=\frac{435 \times 0.4^{0.546}}{22^{1.89}} \times 600 = 460 psig = 460 +14.7 = 474.7 psia</math>
  
−
Note that for the deviated wells TVD depths should be used.
+
Validity check 180/474.7=0.38 < 0.7 OK
  
 
==Nomenclature==
 
==Nomenclature==
−
:<math>g</math> = 9.81, m/s^2
+
:<math>D</math> = choke beam diametr, 64th of an inch
−
:<math>h</math> = depth, m
+
:<math>GLR</math> = gas liquid ratio, Mscf/bbl or 10^3 scf/bbl
−
:<math>H_d</math> = fluid level, m
+
:<math>P_{wh}</math> = well head pressure, psig
−
:<math>H_{perfs}</math> = top of the perforations, m
+
:<math>q</math> = liquid flow rate, bbl/d
−
:<math>H_{pump}</math> = pump setting depth, m
 
−
:<math>P</math> = pressure, atm
 
−
:<math>P_{ann}</math> = annulus presssure, atm
 
−
:<math>P_{wf}</math> = well flowing bottomhole pressure, atm
 
−
:<math>\rho</math> = density, kg/m^3
 
−
:<math>SG_o</math> = oil specific gravity, dimensionless
 
−
:<math>SG_w</math> = water specific gravity, dimensionless
 
−
:<math>WCUT</math> = well water cut, fraction
 
  
 
== References ==
 
== References ==
 
<references>
 
<references>
 +
<ref name= Gilbert>{{cite book
 +
|last1= Gilbert |first1= W.E.
 +
|title=Flowing and Gas-Lift Well Performance
 +
|journal=Drilling and Production Practice API
 +
|date=1954
 +
|page=143
 +
}}</ref>
 
<ref name= KermitBrown1984 >{{cite book
 
<ref name= KermitBrown1984 >{{cite book
 
  |last1= Brown |first1= Kermit
 
  |last1= Brown |first1= Kermit
Line 46: Line 44:
 
  |place=Tulsa, Oklahoma
 
  |place=Tulsa, Oklahoma
 
}}</ref>
 
}}</ref>
−
 
+
<ref name=Economides>{{cite book
 +
|last1= Economides |first1=M.J.
 +
|last2= Hill |first2=A.D.
 +
|last3= Economides |first3=C.E.
 +
|last4= Zhu |first4=D.
 +
|title=Petroleum Production Systems
 +
|edition=2
 +
|date=2013
 +
|publisher=Prentice Hall
 +
|place=Westford, Massachusetts
 +
|isbn=978-0-13-703158-0
 +
}}</ref>
 
</references>
 
</references>
  

Latest revision as of 19:10, 8 November 2024

By Mikhail Tuzovskiy on 20241108191031

Brief

The most common formula used for multiphase flow through surface chokes developed by Gilbert in 1954[1].

Gilbert developed his empirical equation from field data in California[2].

Math and Physics

P_{wh}=\frac{435 \times GLR^{0.546}}{D^{1.89}} \times q

Note that the equation is independent of the downstream pressure and assumes that the downstream pressure is less than 70% of the upstream pressure, i.e. the flow is "critical" i.e. fluid reach sonic velocity in the throat of the choke[3].

Example

Given data

Oil rate = 600 bbl/d, GLR=400 scf/bbl, D=22/64 in, Line pressure = 180 psia

Calculate the well head pressure?

Solution

P_{wh}=\frac{435 \times 0.4^{0.546}}{22^{1.89}} \times 600 = 460 psig = 460 +14.7 = 474.7 psia

Validity check 180/474.7=0.38 < 0.7 OK

Nomenclature

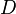D = choke beam diametr, 64th of an inch
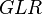GLR = gas liquid ratio, Mscf/bbl or 10^3 scf/bbl
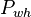P_{wh} = well head pressure, psig
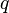q = liquid flow rate, bbl/d

References

  1. ↑ Gilbert, W.E. (1954). Flowing and Gas-Lift Well Performance. Drilling and Production Practice API. p. 143. 
  2. ↑ Brown, Kermit (1984). The Technology of Artificial Lift Methods. Volume 4. Production Optimization of Oil and Gas Wells by Nodal System Analysis. Tulsa, Oklahoma: PennWellBookss. 
  3. ↑ Economides, M.J.; Hill, A.D.; Economides, C.E.; Zhu, D. (2013). Petroleum Production Systems (2 ed.). Westford, Massachusetts: Prentice Hall. ISBN 978-0-13-703158-0. 


Retrieved from "https://wiki.pengtools.com/index.php?title=Gilbert_choke_equation&oldid=7826"