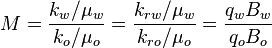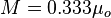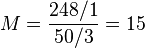Difference between revisions of "Mobility Ratio"
From wiki.pengtools.com
| (9 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
:<math> M > 1</math> water preferentially flows in the reservoir, unstable flow, fingering. | :<math> M > 1</math> water preferentially flows in the reservoir, unstable flow, fingering. | ||
| − | + | ==Equation== | |
:<math> M = \frac{k_w/ \mu_w}{k_o/ \mu_o}=\frac{k_{rw}/ \mu_w}{k_{ro}/ \mu_o}=\frac{q_w B_w}{q_o B_o}</math> | :<math> M = \frac{k_w/ \mu_w}{k_o/ \mu_o}=\frac{k_{rw}/ \mu_w}{k_{ro}/ \mu_o}=\frac{q_w B_w}{q_o B_o}</math> | ||
| Line 18: | Line 18: | ||
:<math> k_o </math> = relative oil phase permeability, function of the phase saturation, mD | :<math> k_o </math> = relative oil phase permeability, function of the phase saturation, mD | ||
:<math> k_w </math> = water phase permeability, function of the phase saturation, mD | :<math> k_w </math> = water phase permeability, function of the phase saturation, mD | ||
| − | :<math> M = mobility ratio, fraction | + | :<math> M </math>= mobility ratio, fraction |
:<math> \mu_o </math> = oil viscosity, cP | :<math> \mu_o </math> = oil viscosity, cP | ||
:<math> \mu_w </math> = water viscosity, cP | :<math> \mu_w </math> = water viscosity, cP | ||
:<math> q_o </math> = oil rate, cc/sec | :<math> q_o </math> = oil rate, cc/sec | ||
:<math> q_w </math> = water rate, cc/sec | :<math> q_w </math> = water rate, cc/sec | ||
| + | |||
| + | Rule of thumb: | ||
| + | :<math> M = 0.333 \mu_o</math> | ||
==Example== | ==Example== | ||
| − | Determine [[Mobility Ratio]] using the following data<ref name=DW/>: | + | Determine the [[Mobility Ratio]] using the following data<ref name=DW/>:<BR> |
| − | Core is 70% water and 30% oil saturation. Water phase permeability is 248 mD, oil phase permeability is 50 mD. Water viscosity is | + | Core is at 70% water and 30% oil saturation. Water phase permeability is 248 mD, oil phase permeability is 50 mD. Water viscosity is 1 cP, oil viscosity is 3 cP. |
:<math> M = \frac{248/1}{50/3} =15 </math> | :<math> M = \frac{248/1}{50/3} =15 </math> | ||
| − | + | In this case the mobility of water is 15 times higher than the mobility of water. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==See Also== | ==See Also== | ||
Latest revision as of 09:02, 4 April 2022
Contents
Brief
Mobility Ratio determines the relative rate of one fluid to another (etc. water to oil).
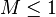oil is dominant flowing phase, stable flow.
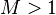water preferentially flows in the reservoir, unstable flow, fingering.
Equation
where
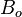= oil formation volume factor, m3/m3
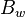= water formation volume factor, m3/m3
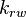= relative water phase permeability, function of the phase saturation, fraction
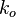= oil phase permeability, function of the phase saturation, fraction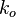- = relative oil phase permeability, function of the phase saturation, mD
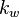= water phase permeability, function of the phase saturation, mD
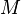= mobility ratio, fraction
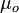= oil viscosity, cP
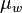= water viscosity, cP
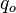= oil rate, cc/sec
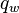= water rate, cc/sec
Rule of thumb:
Example
Determine the Mobility Ratio using the following data[1]:
Core is at 70% water and 30% oil saturation. Water phase permeability is 248 mD, oil phase permeability is 50 mD. Water viscosity is 1 cP, oil viscosity is 3 cP.
In this case the mobility of water is 15 times higher than the mobility of water.
See Also
References
- ↑
Wolcott, Don (2009). Applied Waterflood Field Development
. Houston: Energy Tribune Publishing Inc.
