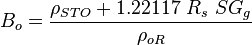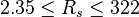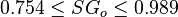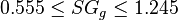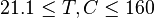Difference between revisions of "McCain Oil Formation Volume Factor equation"
From wiki.pengtools.com
(Created page with "__TOC__ == McCain Oil Formation Volume Factor correlation== McCain correlation is an empirical correlation for the '''oil...") |
(→McCain Oil Formation Volume Factor equation) |
||
| (25 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
__TOC__ | __TOC__ | ||
| − | == McCain Oil Formation Volume Factor | + | == McCain Oil Formation Volume Factor equation== |
| − | [[McCain Oil Formation Volume Factor | + | [[McCain Oil Formation Volume Factor equation|McCain equation]] is determined from material balance equation based on the definition of the '''oil formation volume factor'''<ref name= M1990/>. |
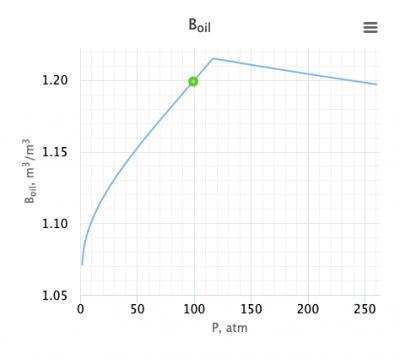
| − | [[File:McCain Oil | + | [[File:McCain Oil Formation Volume Factor equation.png|thumb|right|400px|https://www.pengtools.com/pvtCalculator?paramsToken=de71e4cc29541ab2117e07408864410c|McCain Oil Formation Volume Factor equation in the PVT Software]] |
== Math & Physics == | == Math & Physics == | ||
| − | + | :<math>B_o = \frac{\rho_{STO}+1.22117\ R_s\ SG_g}{\rho_{oR}}</math><ref name=PracticalPVT/> | |
| − | + | == Example. Calculation of the oil formation volume factor == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == Example. Calculation of the oil | ||
Example source <ref name=DW/> | Example source <ref name=DW/> | ||
===Input data=== | ===Input data=== | ||
| − | :<math>R_s</math> = 53.24 | + | :<math>R_s</math> = 53.24 sm<sup>3</sup>/sm<sup>3</sup> at P = 10 MPa |
:<math>SG_o</math> = 0.85 or 35 API | :<math>SG_o</math> = 0.85 or 35 API | ||
:<math>SG_g</math> = 0.75 | :<math>SG_g</math> = 0.75 | ||
| − | :<math> | + | :<math>\rho_{oR}</math> = 749 kg/m<sup>3</sup> at P = 10 MPa |
| − | + | ||
| − | Calculate oil | + | Calculate oil formation oil factor at p = 10 MPa? |
===Solution=== | ===Solution=== | ||
| − | :<math> | + | :<math>B_o</math> = 1.199 rm<sup>3</sup>/sm<sup>3</sup> |
The solution is available in the online PVT calculator software model at [https://www.pengtools.com/pvtCalculator?paramsToken=de71e4cc29541ab2117e07408864410c www.pengtools.com] | The solution is available in the online PVT calculator software model at [https://www.pengtools.com/pvtCalculator?paramsToken=de71e4cc29541ab2117e07408864410c www.pengtools.com] | ||
== Application range == | == Application range == | ||
| − | |||
| − | :<math> | + | :<math> 2.35 \le R_s \le 322 </math> |
| − | + | :<math> 0.754 \le SG_o \le 0.989 </math> | |
| − | + | :<math> 0.555 \le SG_g \le 1.245 </math> | |
| − | :<math> 0. | + | :<math> 21.1 \le T, C \le 160 </math> |
| − | :<math> 0. | ||
| − | :<math> | ||
| − | |||
| − | |||
== Nomenclature == | == Nomenclature == | ||
| − | :<math> | + | :<math> B_o </math> = oil formation volume factor, rm<sup>3</sup>/sm<sup>3</sup> |
| − | + | :<math> R_s </math> = solution gas-oil ratio, sm<sup>3</sup>/sm<sup>3</sup> | |
| − | :<math> R_s </math> = solution gas-oil ratio, | ||
:<math> SG_g </math> = gas specific gravity, dimensionless | :<math> SG_g </math> = gas specific gravity, dimensionless | ||
| − | |||
:<math> SG_o </math> = oil specific gravity, dimensionless | :<math> SG_o </math> = oil specific gravity, dimensionless | ||
| − | + | :<math> \rho_{oR} </math> = oil density at reservoir conditions, kg/m<sup>3</sup> | |
| − | + | :<math> \rho_{STO} = SG_o \times 1000</math> = stock tank oil density, kg/m<sup>3</sup> | |
| − | :<math> \rho_{ | ||
| − | |||
| − | |||
| − | |||
| − | :<math> \rho_{ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== References == | == References == | ||
<references> | <references> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<ref name=M1990>{{cite book | <ref name=M1990>{{cite book | ||
|last1=McCain|first1=W.D. Jr. | |last1=McCain|first1=W.D. Jr. | ||
| Line 119: | Line 52: | ||
|url=http://www.pennwellbooks.com/petroleum/oil-gas-production/the-properties-of-petroleum-fluids-2nd-edition/ | |url=http://www.pennwellbooks.com/petroleum/oil-gas-production/the-properties-of-petroleum-fluids-2nd-edition/ | ||
|ISBN=978-0878143351 | |ISBN=978-0878143351 | ||
| + | }}</ref> | ||
| + | <ref name=PracticalPVT> | ||
| + | {{cite journal | ||
| + | |last1= Afanasyev |first1=Vitaliy | ||
| + | |last2= Moskvin |first2=Igor | ||
| + | |last3= Wolcott |first3=Ken | ||
| + | |last4= McCain |first4=W.D. | ||
| + | |title=Practical PVT Calculations for black oils | ||
| + | |journal=YUKOS publication | ||
| + | |date=2004 | ||
}}</ref> | }}</ref> | ||
<ref name=DW> | <ref name=DW> | ||
| Line 136: | Line 79: | ||
{{#seo: | {{#seo: | ||
| − | |title=McCain Oil | + | |title=McCain Oil Formation Volume Factor equation |
|titlemode= replace | |titlemode= replace | ||
| − | |keywords= | + | |keywords=oil formation volume factor, petroleum engineering, PVT |
| − | |description=McCain Oil | + | |description=McCain Oil Formation Volume Factor equation is determined from material material balance equation based on the definition of the oil formation volume factor |
}} | }} | ||
Latest revision as of 12:37, 28 September 2020
Contents
McCain Oil Formation Volume Factor equation
McCain equation is determined from material balance equation based on the definition of the oil formation volume factor[1].
Math & Physics
Example. Calculation of the oil formation volume factor
Example source [3]
Input data
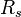 = 53.24 sm3/sm3 at P = 10 MPa
= 53.24 sm3/sm3 at P = 10 MPa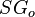 = 0.85 or 35 API
= 0.85 or 35 API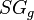 = 0.75
= 0.75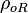 = 749 kg/m3 at P = 10 MPa
= 749 kg/m3 at P = 10 MPa
Calculate oil formation oil factor at p = 10 MPa?
Solution
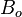 = 1.199 rm3/sm3
= 1.199 rm3/sm3
The solution is available in the online PVT calculator software model at www.pengtools.com
Application range
Nomenclature
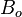 = oil formation volume factor, rm3/sm3
= oil formation volume factor, rm3/sm3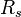 = solution gas-oil ratio, sm3/sm3
= solution gas-oil ratio, sm3/sm3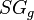 = gas specific gravity, dimensionless
= gas specific gravity, dimensionless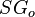 = oil specific gravity, dimensionless
= oil specific gravity, dimensionless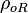 = oil density at reservoir conditions, kg/m3
= oil density at reservoir conditions, kg/m3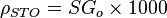 = stock tank oil density, kg/m3
= stock tank oil density, kg/m3
References
- ↑ McCain, W.D. Jr. (1990). Properties of Petroleum Fluids (2 ed.). Oklahoma: PennWell Corp. ISBN 978-0878143351.
- ↑ Afanasyev, Vitaliy; Moskvin, Igor; Wolcott, Ken; McCain, W.D. (2004). "Practical PVT Calculations for black oils". YUKOS publication.
- ↑
Wolcott, Don (2009). Applied Waterflood Field Development
 . Houston: Energy Tribune Publishing Inc.
. Houston: Energy Tribune Publishing Inc.