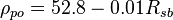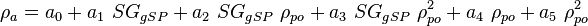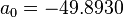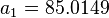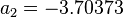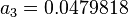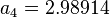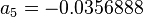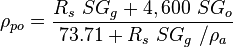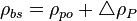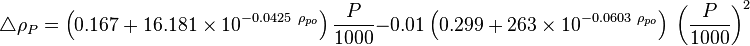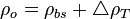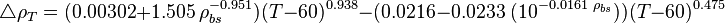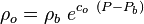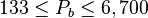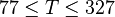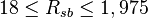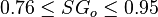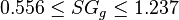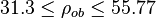Difference between revisions of "McCain Oil density correlation"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Math & Physics)
(→‎Math & Physics)
 
(14 intermediate revisions by the same user not shown)
Line 5: Line 5:
 
[[McCain Oil density correlation|McCain correlation]] is an empirical correlation for the '''oil density''' published in '''1995''' <ref name= M1995/>.
 
[[McCain Oil density correlation|McCain correlation]] is an empirical correlation for the '''oil density''' published in '''1995''' <ref name= M1995/>.
  
−
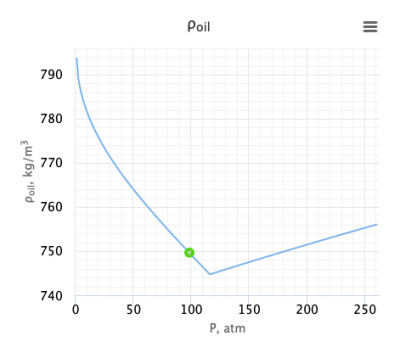
[[File:McCain Oil density.png|thumb|right|400px|https://www.pengtools.com/pvtCalculator?paramsToken=ae54207cce4f303a836f54df9d995152|McCain oil density correlation in the PVT Software]]
+
[[File:McCain Oil density.png|thumb|right|400px|https://www.pengtools.com/pvtCalculator?paramsToken=de71e4cc29541ab2117e07408864410c|McCain oil density correlation in the PVT Software]]
  
 
== Math & Physics ==
 
== Math & Physics ==
Line 15: Line 15:
 
Apparent liquid density:
 
Apparent liquid density:
  
−
:<math>\rho_a = a_0 + a_1\ SG_g_SP + a_2\ SG_g_SP\ \rho_{po} + a_3\ SG_g_SP\ \rho_{po}^2 + a_4\ \rho_{po} +a_5\ \rho_{po}^2 </math>
+
:<math>\rho_a = a_0 + a_1\ SG_{gSP} + a_2\ SG_{gSP}\ \rho_{po} + a_3\ SG_{gSP}\ \rho_{po}^2 + a_4\ \rho_{po} +a_5\ \rho_{po}^2 </math>
 
:<math>a_0 = -49.8930</math>
 
:<math>a_0 = -49.8930</math>
 
:<math>a_1 = 85.0149</math>
 
:<math>a_1 = 85.0149</math>
Line 23: Line 23:
 
:<math>a_5 =- 0.0356888</math>
 
:<math>a_5 =- 0.0356888</math>
  
−
Next pseudoliquid density:
+
Next pseudoliquid density<ref name= M1990/>:
−
:<math>\rho_{po} = \frac{R_s\ SG_g + 4,600\ SG_o}{73.71+R_s\ SG_g\ / \rho_a}</math><ref name= M1990/>
+
:<math>\rho_{po} = \frac{R_s\ SG_g + 4,600\ SG_o}{73.71+R_s\ SG_g\ / \rho_a}</math>
  
 
Iterate until pseudoliquid densities are equal.
 
Iterate until pseudoliquid densities are equal.
Line 34: Line 34:
 
where
 
where
  
−
:<math>\triangle \rho_{P} = \left ( 0.617 + 16.181 \times 10^{-0.0425\ \rho_{po}} \right) \frac{P}{1000} - 0.01 \left ( 0.299 + 263 \times 10^{-0.0603\ \rho_{po}}\right)\ \left (\frac{P}{1000}\right)^2 </math>
+
:<math>\triangle \rho_{P} = \left ( 0.167 + 16.181 \times 10^{-0.0425\ \rho_{po}} \right) \frac{P}{1000} - 0.01 \left ( 0.299 + 263 \times 10^{-0.0603\ \rho_{po}}\right)\ \left (\frac{P}{1000}\right)^2 </math>
  
 
Adjust density to the temperature of interest:
 
Adjust density to the temperature of interest:
Line 47: Line 47:
  
 
:<math>\rho_{o} = \rho_{b}\ e^{c_o\ (P - P_b)} </math>
 
:<math>\rho_{o} = \rho_{b}\ e^{c_o\ (P - P_b)} </math>
 +
 +
== Example. Calculation of the oil density ==
 +
Example source <ref name=DW/>
 +
===Input data===
 +
:<math>R_s</math> = 53.24 sm3/sm3
 +
:<math>SG_o</math> = 0.85 or 35 API
 +
:<math>SG_g</math> = 0.75
 +
:<math>T</math> = 90C or 363K
 +
:<math>P</math> = 10 MPa
 +
Calculate oil density at p = 10 MPa?
 +
 +
===Solution===
 +
:<math>\rho_o</math> = 749.645 kg/m3
 +
 +
The solution is available in the online PVT calculator software model at [https://www.pengtools.com/pvtCalculator?paramsToken=de71e4cc29541ab2117e07408864410c www.pengtools.com]
  
 
== Application range ==
 
== Application range ==
Line 65: Line 80:
 
:<math> R_s </math> =  solution gas-oil ratio, scf/stb
 
:<math> R_s </math> =  solution gas-oil ratio, scf/stb
 
:<math> SG_g </math> = gas specific gravity, dimensionless
 
:<math> SG_g </math> = gas specific gravity, dimensionless
 +
:<math> SG_{gSP} </math> = gas specific gravity at separator pressure, dimensionless
 
:<math> SG_o </math> = oil specific gravity, dimensionless
 
:<math> SG_o </math> = oil specific gravity, dimensionless
 
:<math> T </math> = temperature, °F
 
:<math> T </math> = temperature, °F
  
 
:<math> \rho_{a} </math> = apparent density of surface gas if it were a liquid, lb<sub>m</sub>/ft<sup>3</sup>
 
:<math> \rho_{a} </math> = apparent density of surface gas if it were a liquid, lb<sub>m</sub>/ft<sup>3</sup>
 +
:<math> \rho_{ob} </math> = liquid density at the bubble point pressure, lb<sub>m</sub>/ft<sup>3</sup>
 
:<math> \rho_{bs} </math> = liquid density at reservoir pressure and 60°F, lb<sub>m</sub>/ft<sup>3</sup>
 
:<math> \rho_{bs} </math> = liquid density at reservoir pressure and 60°F, lb<sub>m</sub>/ft<sup>3</sup>
 
:<math> \rho_o </math> = oil density, lb<sub>m</sub>/ft<sup>3</sup>
 
:<math> \rho_o </math> = oil density, lb<sub>m</sub>/ft<sup>3</sup>
Line 103: Line 120:
 
  |ISBN=978-0878143351
 
  |ISBN=978-0878143351
 
}}</ref>
 
}}</ref>
−
 
+
<ref name=DW>
 +
{{cite book
 +
|last1= Wolcott |first1=Don
 +
|title=Applied Waterflood Field Development
 +
|date=2009
 +
|publisher=Energy Tribune Publishing Inc
 +
|place=Houston
 +
|url=https://www.amazon.com/Applied-Waterflood-Field-Development-Wolcott/dp/0578023946/ref=sr_1_1?ie=UTF8&qid=1481788841&sr=8-1&keywords=Don+wolcott
 +
|url-access=subscription
 +
}}</ref>
 
</references>
 
</references>
  

Latest revision as of 18:41, 23 November 2023

McCain Oil density correlation

McCain correlation is an empirical correlation for the oil density published in 1995 [1].

McCain oil density correlation in the PVT Software

Math & Physics

Pseudoliquid density:

\rho_{po} = 52.8 - 0.01 R_{sb}

Apparent liquid density:

\rho_a = a_0 + a_1\ SG_{gSP} + a_2\ SG_{gSP}\ \rho_{po} + a_3\ SG_{gSP}\ \rho_{po}^2 + a_4\ \rho_{po} +a_5\ \rho_{po}^2
a_0 = -49.8930
a_1 = 85.0149
a_2 = - 3.70373
a_3 = 0.0479818
a_4 = 2.98914
a_5 =- 0.0356888

Next pseudoliquid density[2]:

\rho_{po} = \frac{R_s\ SG_g + 4,600\ SG_o}{73.71+R_s\ SG_g\ / \rho_a}

Iterate until pseudoliquid densities are equal.

Next adjust density to the pressure of interest:

\rho_{bs} = \rho_{po} + \triangle \rho_P

where

\triangle \rho_{P} = \left ( 0.167 + 16.181 \times 10^{-0.0425\ \rho_{po}} \right) \frac{P}{1000} - 0.01 \left ( 0.299 + 263 \times 10^{-0.0603\ \rho_{po}}\right)\ \left (\frac{P}{1000}\right)^2

Adjust density to the temperature of interest:

\rho_{o} = \rho_{bs} + \triangle \rho_T

where

\triangle \rho_T = (0.00302 + 1.505\ \rho_{bs}^{-0.951}) (T - 60)^{0.938} - (0.0216 - 0.0233\ (10^{-0.0161\ \rho_{bs}})) (T - 60)^{0.475}

Oil density above the bubble point pressure:

\rho_{o} = \rho_{b}\ e^{c_o\ (P - P_b)}

Example. Calculation of the oil density

Example source [3]

Input data

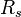R_s = 53.24 sm3/sm3
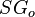SG_o = 0.85 or 35 API
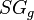SG_g = 0.75
T = 90C or 363K
P = 10 MPa

Calculate oil density at p = 10 MPa?

Solution

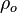\rho_o = 749.645 kg/m3

The solution is available in the online PVT calculator software model at www.pengtools.com

Application range

Description of the Data Used[1]:

133 \le P_b \le 6,700
77 \le T \le 327
18 \le R_{sb} \le 1,975
0.76 \le SG_o \le 0.95
0.556 \le SG_g \le 1.237
31.3 \le \rho_{ob} \le 55.77

Number of data sets = 684

Nomenclature

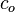c_o = oil compressibility, 1/psia
P = pressure, psia
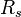R_s = solution gas-oil ratio, scf/stb
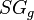SG_g = gas specific gravity, dimensionless
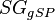SG_{gSP} = gas specific gravity at separator pressure, dimensionless
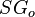SG_o = oil specific gravity, dimensionless
T = temperature, °F
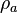\rho_{a} = apparent density of surface gas if it were a liquid, lbm/ft3
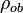\rho_{ob} = liquid density at the bubble point pressure, lbm/ft3
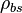\rho_{bs} = liquid density at reservoir pressure and 60°F, lbm/ft3
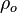\rho_o = oil density, lbm/ft3
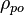\rho_{po} = pseudoliquid formed by recombination of surface gas and liquid at standard conditions, lbm/ft3
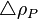\triangle \rho_{P} = adjustment to liquid density due to pressure, lbm/ft3
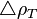\triangle \rho_{T} = adjustment to liquid density due to temperature, lbm/ft3

Subscripts

b - bubble point
g - gas
o - oil

References

  1. ↑ 1.0 1.1 McCain, W.D. Jr.; Hill, N. C. (1995). "Correlations for Liquid Densities and Evolved Gas Specific Gravities for Black Oils During Pressure Depletion"Free registration required. Society of Petroleum Engineers (SPE-30773-MS). 
  2. ↑ McCain, W.D. Jr. (1990). Properties of Petroleum Fluids (2 ed.). Oklahoma: PennWell Corp. ISBN 978-0878143351. 
  3. ↑ Wolcott, Don (2009). Applied Waterflood Field DevelopmentPaid subscription required. Houston: Energy Tribune Publishing Inc. 
Retrieved from "https://wiki.pengtools.com/index.php?title=McCain_Oil_density_correlation&oldid=7718"