Difference between revisions of "Category: OnPlan"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Math & Physics)
(→‎Main features)
 
(40 intermediate revisions by the same user not shown)
Line 4: Line 4:
 
[[File:onPlan_i.png|thumb|right|200px|link=https://www.pengtools.com/onPlan|pengtools onPlan]]
 
[[File:onPlan_i.png|thumb|right|200px|link=https://www.pengtools.com/onPlan|pengtools onPlan]]
  
−
[[:Category:onPlan| onPlan]] is a fracture simulation tool for designing a hydraulic fracture treatment.
+
[[:Category:onPlan| onPlan]] is a hydraulic fracture simulation software for designing a hydraulic fracture treatment.
  
−
[[:Category:onPlan| onPlan]] is developed under cooperation agreement between [[:category:pengtools | pengtools]] and [https://mipt.ru/education/chair/applied_mechanics/ Moscow Institute of Physics and Technology Oil&Gas Center LLC].
+
[[:Category:onPlan| onPlan]] is released under cooperation agreement between [[:category:pengtools | pengtools]] and [https://mipt.ru/education/chair/applied_mechanics/ Moscow Institute of Physics and Technology Oil&Gas Center LLC].
  
 
[[:Category:onPlan| onPlan]] utilizes the Planar3D class model with advanced numerical optimization which allows to achieve high accuracy in predicting fracture geometry and fast simulation time.
 
[[:Category:onPlan| onPlan]] utilizes the Planar3D class model with advanced numerical optimization which allows to achieve high accuracy in predicting fracture geometry and fast simulation time.
Line 16: Line 16:
 
== Typical applications ==
 
== Typical applications ==
  
−
* Simulation of the single vertical well fractures in low stress contrast environments with a high risk of fracture breakthrough into overlying gas or underlying water
+
* Simulation of a single vertical well fractures in low stress contrast environments with a high risk of fracture breakthrough into overlying gas or underlying water
 
* Optimization of hydraulic fracturing with '''Unified Fracture Design'''<ref name=UFD2002/>
 
* Optimization of hydraulic fracturing with '''Unified Fracture Design'''<ref name=UFD2002/>
 
* Understanding post-fracturing production performance
 
* Understanding post-fracturing production performance
 
* Sensitivity studies
 
* Sensitivity studies
−
 
−
== Main features ==
 
−
* Fracture design charts: height, width, length, pressure vs time; height vs width; width vs length; height vs length. All showing propped and hydraulic values.
 
−
* Fracture design Type Curves (Plot of '''J<sub>D</sub>''' as a function of '''C<sub>fD</sub>''' using '''I<sub>x</sub>''' and '''N<sub>p</sub>''' as parameter) showing the current fracture design and the optimal one.
 
−
* Design Optimization Curve which corresponds to the maximum '''J<sub>D</sub>''' values for different '''N<sub>p</sub>'''.
 
−
* Design Optimum Point at which '''J<sub>D</sub>''' is maximized for the given proppant, fracture and reservoir parameters.
 
−
* Physical constraints envelope.
 
−
* [[Proppant catalog]] with predefined proppant properties.
 
−
* Users reference data for benchmarking vs actual.
 
−
* Switch between Metric and Field units
 
−
* Save/load models to the files and to the user’s cloud
 
−
* Share models to the public cloud or by using model’s link
 
−
* Export pdf report containing input parameters, calculated values and plots
 
−
* Continue your work from where you stopped: last saved model will be automatically opened
 
−
* Download the chart as an image or data and print (upper-right corner chart’s button)
 
−
* Export results table to Excel or other application
 
  
 
==Math & Physics==
 
==Math & Physics==
Line 46: Line 30:
 
:<math>\frac{\partial}{\partial t} h C_i + div q_i = v_i\ and\ V_p = V_p + \Delta V</math> (  2  ) - 2D equation of multifluid flow and proppant transport
 
:<math>\frac{\partial}{\partial t} h C_i + div q_i = v_i\ and\ V_p = V_p + \Delta V</math> (  2  ) - 2D equation of multifluid flow and proppant transport
  
−
The model accounts for the effect of proppant bridging and gravitational setting.
+
The model accounts for the effect of proppant bridging, gravitational setting and multifluid flow.
  
−
The mathematical model is supplemented by rheological dependencies for coupling the flow of a fluid with a pressure gradient and equations for calculating leaks into the reservoir.
+
The mathematical model is supplemented by rheological dependencies for coupling the flow of a fluid with a pressure gradient and equations for calculating leak-off to the reservoir.
  
 
===Splitting by physical processes===
 
===Splitting by physical processes===
 
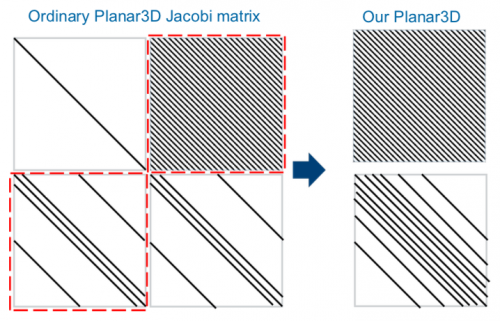
In usual numerical Planar3D implementation, Jacobi matrix includes parts that describe geomechanical and hydrodynamical processes. Splitting by physical processes allows to solve geomechanics and hydrodynamics separately. Splitting turns one linear system with dense matrix into two. Separate solving requires significantly less computation resources than solving whole system.
 
In usual numerical Planar3D implementation, Jacobi matrix includes parts that describe geomechanical and hydrodynamical processes. Splitting by physical processes allows to solve geomechanics and hydrodynamics separately. Splitting turns one linear system with dense matrix into two. Separate solving requires significantly less computation resources than solving whole system.
  
−
==Type Curves==
+
==MIPT developers==
  
−
The Type Curves shows the dimensionless productivity index, '''J<sub>D</sub>''',  at steady and pseudo-steady state as function of  '''C<sub>fD</sub>''', using '''I<sub>x</sub>''' as parameter (red curves) and overlapping with the type curve with '''N<sub>p</sub>''' as parameter (black curves).
+
[https://mipt.ru/english/ Moscow Institute of Physics and Technology]
  
−
The green curve along the maximum points for different '''N<sub>p</sub>''' values is “Design Optimization Curve”<ref name = pushing/>. This curve represents the target of the designs of the fracture treatments in a dimensionless form.
+
[https://mipt.ru/science/labs/laboratoriya-modelirovaniya-mekhanicheskikh-sistem-i-protsessov/ Laboratory of Modeling of Mechanical Systems and Processes]
  
−
[[File:pseudo-steady state type curve.png | link=https://www.pengtools.com/optiFrac | Open in optiFrac]]
+
[[File:Natalia Zavialova.jpg|300px| Natalia Zavialova]]
  
−
[[File:steady state type curve.png  | link=https://www.pengtools.com/optiFrac | Open in optiFrac]]
+
[[File:Ilia Perepechkin.jpg|300px| Ilia Perepechkin]]
  
−
Type Curves were obtained, through seven hundred runs with a numerical simulator, modeling a fractured well in a closed square reservoir <ref name = pushing/>. For infinite and finite fracture conductivities, the shape factors, '''C<sub>A</sub>''', can be calculated if the '''P<sub>D</sub>''' is known for a specific value of '''I<sub>x</sub>'''. The '''P<sub>D</sub>''' value obtained by numerical simulations. After knowing '''C<sub>A</sub>''' (which would be a function of  '''I<sub>x</sub>'''), f-function values can be calculated if  '''P<sub>D</sub>''' is known for a specific dimensionless fracture conductivity '''C<sub>fD</sub>''' and fracture penetration  '''I<sub>x</sub>'''.
+
== Comparison Studies ==
  
−
==Flow Diagram==
+
[[File:Weng Case B.png|300px| Weng Case B]]
  
−
[[File:optiFrac flow diagram.png|400px]]
+
1. [[OnPlan Comparison Study 1 Weng]]. The onPlan calculates 12 cases described in the paper and shows reasonable agreement in results.
  
−
==Workflow==
+
[[File:Warpinski Case 5.png|600px| Warpinski Case 5 (5-Layer 200cp)]]
  
−
[[File:Fracturedimensions.png|thumb|right|500px| Fracture Plane Dimensions]]
+
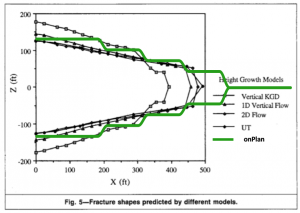
2. [[OnPlan Comparison Study 2 Warpinski]].
  
−
1. Calculate the '''N<sub>p</sub>''':
+
== Main page screenshot ==
  
−
:<math>V_r=h_{net} {x_e}^2</math> the volume of the reservoir
+
[[File:onPlan main page.png|800px| onPlan main page]]
  
−
:<math>k_f=k_{prop} * Gel Damage</math> the fracture permeability
+
== Main features ==
−
 
+
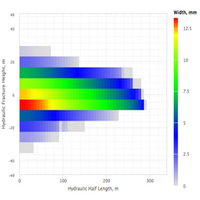
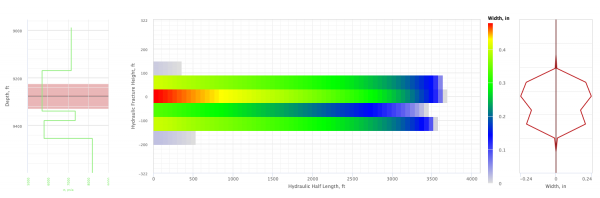
* Fracture design charts: height, width, length, pressure vs time; height vs width; width vs length; height vs length. All showing propped and hydraulic values.
−
:<math>M_f=\frac{M_{prop}}{Out Zone Growth} \frac{h_{net}}{h_{gross}}</math> the proppant mass in the pay zone
+
* Fracture design Type Curves (Plot of '''J<sub>D</sub>''' as a function of '''C<sub>fD</sub>''' using '''I<sub>x</sub>''' and '''N<sub>p</sub>''' as parameter) showing the current fracture design and the optimal one.
−
 
+
* Design Optimization Curve which corresponds to the maximum '''J<sub>D</sub>''' values for different '''N<sub>p</sub>'''.
−
:<math>V_f=\frac{M_f}{SG_{prop} (1 - \phi_{prop})}</math> the fracture volume in the pay zone
+
* Design Optimum Point at which '''J<sub>D</sub>''' is maximized for the given proppant, fracture and reservoir parameters.
−
 
+
* Physical constraints envelope.
−
:<math>N_p=\frac{2 k_f V_f}{k V_r}</math> the proppant number
+
* [[Hydraulic fracturing proppant catalog]] with predefined proppant properties.
−
 
+
* Users reference data for benchmarking vs actual.
−
2. Read '''C<sub>fD</sub><sup>opt</sup>''', '''I<sub>x</sub><sup>opt</sup>''', '''J<sub>D</sub><sup>opt</sup>''' from the Design Optimization Curve of the Type Curve
+
* Switch between Metric and Field units
−
 
+
* Save/load models to the files and to the user’s cloud
−
3. Calculate optimum fracture half-length and width:
+
* Share models to the public cloud or by using model’s link
−
 
+
* Export pdf report containing input parameters, calculated values and plots
−
:<math>{x_f}^{opt}=0.5 x_e {I_x}^{opt}</math>
+
* Continue your work from where you stopped: last saved model will be automatically opened
−
 
+
* Download the chart as an image or data and print (upper-right corner chart’s button)
−
:<math>{w_f}^{opt}=\frac{{C_{fD}}^{opt} {x_f}^{opt} k}{k_f}</math>
+
* Export results table to Excel or other application
−
 
 
−
:<math>h_f=h_{gross} * Out Zone Growth</math> the fracture height
 
−
 
 
−
==Physical Constraints==
 
−
It is important to mention that the Design Optimization Curve could give unrealistic fracture geometry depending on the reservoir permeability, reservoir mechanical properties and target '''N<sub>p</sub>'''. The two most common scenarios are <ref name = pushing/>:
 
−
 
 
−
# The required net pressure for the fracture geometry is too high - “maximum net pressure curve”,
 
−
# Fracture width is too small (fracture too narrow) - “minimum width curve”.
 
−
 
 
−
 
 
−
The area between the “minimum width curve” and the “maximum net pressure curve” is the “working area” (highlighted in yellow) of the whole type curve for the specific rock mechanical properties, reservoir and proppant properties used. Any fracture design for this specific case should be located on the “optimum design curve” anywhere in this working area depending on the desired '''N<sub>p</sub>'''<ref name = pushing/>.
 
−
 
 
−
[[File:Physical Constraints on a PSS type curve.png  | link=https://www.pengtools.com/optiFrac | Open in optiFrac]]
 
−
 
 
−
====Maximum net pressure====
 
−
The maximum net pressure during the fracturing treatment should provide a surface pressure less than a certain value (which is surface pressure operational limit) <ref name = pushing/>.
 
−
 
 
−
:<math>w_{max}=\frac{2 P_{net} h_f (1 - \nu^2)}{E}</math>
 
−
 
 
−
:<math>w=w_{max} \frac{\pi}{4} \gamma \delta</math>
 
−
 
 
−
====Minimum fracture width====
 
−
Fracture propped width should be greater than N times mean proppant diameter (to provide at least N proppant layers in the fracture after closure)<ref name = pushing/>. N=3 in the [[:Category:optiFrac | optiFrac]].
 
−
 
 
−
== Nomenclature ==
 
−
:<math>C_{fD}</math> = dimensionless fracture conductivity, dimensionless
 
−
:<math>C_A</math> = shape factor, dimensionless
 
−
:<math>E</math> = Young's Modulus, psia
 
−
:<math>f</math> = f-function, dimensionless
 
−
:<math>Gel Damage</math> = proppant permeability reduction due to gel damage, %
 
−
:<math>h</math> = height, ft
 
−
:<math>I_x</math> = penetration ratio, dimensionless
 
−
:<math>J_D</math> = dimensionless productivity index, dimensionless
 
−
:<math>k</math> = permeability, md
 
−
:<math>M</math> = mass, lbm
 
−
:<math>N_p</math> = dimensionless proppant number, dimensionless
 
−
:<math>Out Zone Growth</math> = out of the zone growth, 0% - no growth, 50% - half of proppant is out of zone
 
−
:<math>\bar{P}_D</math> = dimensionless pressure (based on average pressure), dimensionless
 
−
:<math>P_{net}</math> = net pressure, psia
 
−
:<math>SG</math> = specific gravity, dimensionless
 
−
:<math>V</math> = volume, ft<sup>3</sup>
 
−
:<math>w</math> = width, ft
 
−
:<math>x_e</math> = drainage area, ft<sup>2</sup>
 
−
:<math>x_f</math> = fracture half-length, ft
 
−
 
 
−
===Greek symbols===
 
−
:<math>\delta</math> = dry to wet width ratio at the end of pumping, usually 0.5-0.7
 
−
:<math>\gamma</math> = geometric factor in vertical direction, 0.75 for PKN model, 1 for KGD model
 
−
:<math>\nu</math> = Poisson's ratio, dimensionless
 
−
:<math>\phi</math> = porosity, fraction
 
−
:<math>\pi</math> = 3.1415
 
−
 
 
−
===Superscripts===
 
−
:opt = optimal
 
−
:pss = pseudo-steady state
 
−
:ss = steady state
 
−
 
 
−
===Subscripts===
 
−
:e = external
 
−
:f = fracture
 
−
:gross = gross
 
−
:max = maximum
 
−
:net = net
 
−
:prop = proppant
 
−
:r = reservoir
 
  
 
== References ==
 
== References ==
 
<references>
 
<references>
−
<ref name= pushing >{{cite journal
 
−
|last1=Rueda|first1=J.I.
 
−
|last2=Mach|first2=J.
 
−
|last3=Wolcott|first3=D.
 
−
|title=Pushing Fracturing Limits to Maximize Producibility in Turbidite Formations in Russia
 
−
|publisher=Society of Petroleum Engineers
 
−
|number=SPE-91760-MS
 
−
|date=2004
 
−
|url=https://www.onepetro.org/conference-paper/SPE-91760-MS
 
−
|url-access=registration
 
−
}}</ref>
 
−
 
 
<ref name=UFD2002>{{cite book
 
<ref name=UFD2002>{{cite book
 
  |last1= Economides |first1= Michael J.
 
  |last1= Economides |first1= Michael J.
Line 185: Line 92:
 
</references>
 
</references>
 
[[Category:pengtools]]
 
[[Category:pengtools]]
 +
 +
{{#seo:
 +
|title=Hydraulic Fracturing Simulation Software
 +
|titlemode= replace
 +
|keywords= simulator, hydraulic fracturing, hydraulic fracturing simulation software, hydraulic fracturing formulas, hydraulic fracturing proppant, hydraulic fracturing liquids, petroleum engineering, planar 3D
 +
|description=onPlan is a planar 3D hydraulic fracture simulation software for designing a hydraulic fracture treatment in pengtools.
 +
}}

Latest revision as of 06:30, 10 December 2018

Brief

pengtools onPlan

onPlan is a hydraulic fracture simulation software for designing a hydraulic fracture treatment.

onPlan is released under cooperation agreement between pengtools and Moscow Institute of Physics and Technology Oil&Gas Center LLC.

onPlan utilizes the Planar3D class model with advanced numerical optimization which allows to achieve high accuracy in predicting fracture geometry and fast simulation time.

onPlan integrates the Unified Fracture Design[1] concept which enables comparison of the designed frac geometry with the optimal one to maximize the performance of the fractured well.

onPlan is available online at www.pengtools.com.

Typical applications

  • Simulation of a single vertical well fractures in low stress contrast environments with a high risk of fracture breakthrough into overlying gas or underlying water
  • Optimization of hydraulic fracturing with Unified Fracture Design[1]
  • Understanding post-fracturing production performance
  • Sensitivity studies

Math & Physics

Splitting by physical processes

Basic equations of Planar3D model:

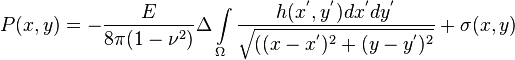P(x,y)=-\frac{E}{8\pi(1-\nu^2)}\Delta \int \limits_{\Omega}^{}\frac{h(x^', y^')dx^'dy^'}{ \sqrt{((x-x^')^2+(y-y^')^2}} + \sigma (x,y) ( 1 ) - elastic reaction of formation
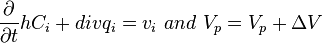\frac{\partial}{\partial t} h C_i + div q_i = v_i\ and\ V_p = V_p + \Delta V ( 2 ) - 2D equation of multifluid flow and proppant transport

The model accounts for the effect of proppant bridging, gravitational setting and multifluid flow.

The mathematical model is supplemented by rheological dependencies for coupling the flow of a fluid with a pressure gradient and equations for calculating leak-off to the reservoir.

Splitting by physical processes

In usual numerical Planar3D implementation, Jacobi matrix includes parts that describe geomechanical and hydrodynamical processes. Splitting by physical processes allows to solve geomechanics and hydrodynamics separately. Splitting turns one linear system with dense matrix into two. Separate solving requires significantly less computation resources than solving whole system.

MIPT developers

Moscow Institute of Physics and Technology

Laboratory of Modeling of Mechanical Systems and Processes

Natalia Zavialova

Ilia Perepechkin

Comparison Studies

Weng Case B

1. OnPlan Comparison Study 1 Weng. The onPlan calculates 12 cases described in the paper and shows reasonable agreement in results.

Warpinski Case 5 (5-Layer 200cp)

2. OnPlan Comparison Study 2 Warpinski.

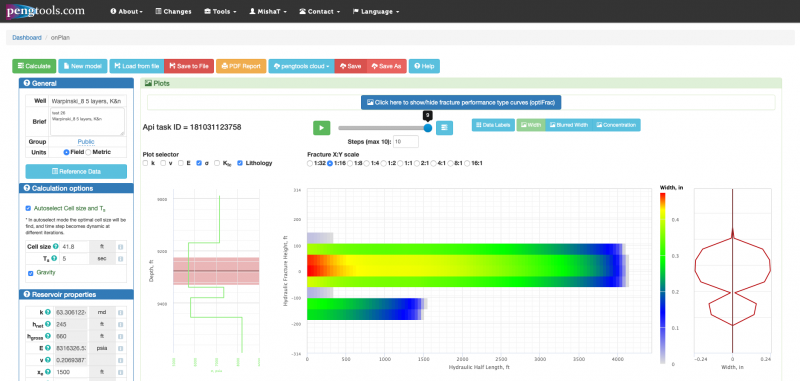
Main page screenshot

onPlan main page

Main features

  • Fracture design charts: height, width, length, pressure vs time; height vs width; width vs length; height vs length. All showing propped and hydraulic values.
  • Fracture design Type Curves (Plot of JD as a function of CfD using Ix and Np as parameter) showing the current fracture design and the optimal one.
  • Design Optimization Curve which corresponds to the maximum JD values for different Np.
  • Design Optimum Point at which JD is maximized for the given proppant, fracture and reservoir parameters.
  • Physical constraints envelope.
  • Hydraulic fracturing proppant catalog with predefined proppant properties.
  • Users reference data for benchmarking vs actual.
  • Switch between Metric and Field units
  • Save/load models to the files and to the user’s cloud
  • Share models to the public cloud or by using model’s link
  • Export pdf report containing input parameters, calculated values and plots
  • Continue your work from where you stopped: last saved model will be automatically opened
  • Download the chart as an image or data and print (upper-right corner chart’s button)
  • Export results table to Excel or other application

References

  1. ↑ 1.0 1.1 Economides, Michael J.; Oligney, Ronald; Valko, Peter (2002). Unified Fracture Design: Bridging the Gap Between Theory and Practice. Alvin, Texas: Orsa Press. 

Pages in category "OnPlan"

The following 4 pages are in this category, out of 4 total.

H

O

Retrieved from "https://wiki.pengtools.com/index.php?title=Category:OnPlan&oldid=5585"