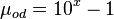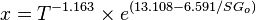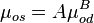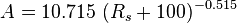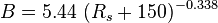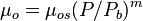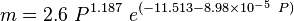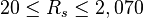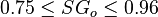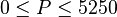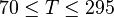Difference between revisions of "Beggs and Robinson Oil Viscosity correlation"
From wiki.pengtools.com
Gprotsykov (talk | contribs) (Created page with "__TOC__ === Brief === Beggs - Robinson correlation is ... === Math & Physics === Dead oil viscosity: :<math>\mu_{od} = 10^X-1</math><ref name= {Beggs - Robinson}/> w...") |
(→Beggs and Robinson Oil Viscosity correlation) |
||
| (53 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
__TOC__ | __TOC__ | ||
| − | == | + | == Beggs and Robinson Oil Viscosity correlation == |
| − | [[Beggs | + | [[Beggs and Robinson Oil Viscosity correlation|Beggs and Robinson]] is an empirical correlation for the '''oil viscosity''' published in '''1975''' <ref name= BR1975/>. |
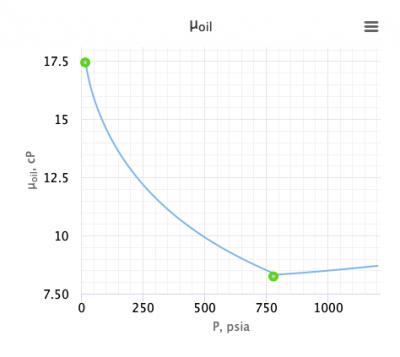
| − | === Math & Physics | + | [[File:Beggs and Robinson.png|thumb|right|400px|link=https://www.pengtools.com/pvtCalculator?paramsToken=b79727e91f05b72cbb6d99afcb588636|Beggs and Robinson oil viscosity correlation in the PVT Software]] |
| + | |||
| + | == Math & Physics == | ||
Dead oil viscosity: | Dead oil viscosity: | ||
| − | :<math>\mu_{od} = 10^ | + | :<math>\mu_{od} = 10^x-1</math> |
where: | where: | ||
| − | + | :<math>x = T^{-1.163} \times e^{(13.108-6.591/SG_{o})}</math> | |
| − | |||
| − | |||
| − | + | Saturated oil viscosity (P < P<sub>b</sub>): | |
| − | + | :<math>\mu_{os} = A \mu_{od}^B</math> | |
| − | :<math>\ | + | where: |
| + | |||
| + | :<math> A = 10.715\ (R_s + 100)^{-0.515} </math> | ||
| + | |||
| + | :<math> B = 5.44\ (R_s + 150)^{-0.338} </math> | ||
| + | |||
| + | Undersaturated oil viscosity (P > P<sub>b</sub>): | ||
| + | |||
| + | :<math>\mu_{o} = \mu_{os} (P/P_b)^m </math><ref name=VB1980/> | ||
where: | where: | ||
| − | |||
| − | |||
| − | |||
| − | :<math> \ | + | :<math>m = 2.6\ P^{1.187}\ e^{(-11.513-8.98 \times 10^{-5}\ P)}</math> |
| + | |||
| + | == Example. Calculation of the oil viscosity == | ||
| + | Example source <ref name=1987PEH/> | ||
| + | ===Input data=== | ||
| + | :<math>T</math> = 137 F° | ||
| + | :<math>SG_o</math> = 0.922 or 22 API | ||
| + | :<math>R_s</math> = 90 scf/stb | ||
| + | |||
| + | Calculate the saturated oil viscosity? | ||
| + | |||
| + | ===Solution=== | ||
| + | x = 1.2658 | ||
| + | :<math>\mu_{od}</math> = 17.44 cP | ||
| + | A = 0.719 | ||
| + | B = 0.853 | ||
| + | :<math>\mu_o</math> = 8.24 cP | ||
| + | |||
| + | The solution is available in the online PVT calculator software model at [https://www.pengtools.com/pvtCalculator?paramsToken=b79727e91f05b72cbb6d99afcb588636 www.pengtools.com] | ||
| − | + | == Application range == | |
| − | + | Description of the Data Used<ref name= BR1975/>: | |
| − | |||
| − | :<math> \ | + | :<math> 20 \le R_s \le 2,070 </math> |
| + | :<math> 0.75 \le SG_o \le 0.96 </math> | ||
| + | :<math> 0 \le P \le 5250 </math> | ||
| + | :<math> 70 \le T \le 295 </math> | ||
| − | = | + | Number of oil systems = 600<BR/> |
| − | + | Number of dead oil observations = 460<BR/> | |
| − | + | Number of live oil observations = 2,073<BR/> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === References | + | == Nomenclature == |
| + | :<math> A </math> = coefficient | ||
| + | :<math> B </math> = coefficient | ||
| + | :<math> m </math> = coefficient | ||
| + | :<math> P </math> = pressure, psia | ||
| + | :<math> R_s </math> = solution gas-oil ratio, scf/stb | ||
| + | :<math> SG_o </math> = oil specific gravity, dimensionless | ||
| + | :<math> T </math> = temperature, °F | ||
| + | :<math> x </math> = coefficient | ||
| + | |||
| + | :<math> \mu </math> = viscosity, cP | ||
| + | |||
| + | ====Subscripts==== | ||
| + | :b - bubble point <BR/> | ||
| + | :od - dead oil <BR/> | ||
| + | :os - saturated oil <BR/> | ||
| + | :o - undersaturated oil <BR/> | ||
| + | |||
| + | == References == | ||
<references> | <references> | ||
| − | <ref name={Beggs - | + | <ref name=BR1975>{{cite journal |
| + | |last1=Beggs|first1=H. D. | ||
| + | |last2= Robinson |first2=J. R. | ||
| + | |title=Estimating the Viscosity of Crude Oil Systems | ||
| + | |journal=Journal of Petroleum Technology | ||
| + | |number=SPE-5434-PA | ||
| + | |date=September 1975 | ||
| + | |volume=27(09) | ||
| + | |url=https://www.onepetro.org/journal-paper/SPE-5434-PA | ||
| + | |url-access=registration | ||
| + | }}</ref> | ||
| + | |||
| + | <ref name=VB1980> | ||
{{cite journal | {{cite journal | ||
| − | |last1= | + | |last1= Vasquez |first1=M. |
|last2= Beggs |first2=H.D. | |last2= Beggs |first2=H.D. | ||
|title=Correlations for Fluid Physical Property Prediction. | |title=Correlations for Fluid Physical Property Prediction. | ||
| Line 62: | Line 107: | ||
|url=https://www.onepetro.org/journal-paper/SPE-6719-PA | |url=https://www.onepetro.org/journal-paper/SPE-6719-PA | ||
|url-access=registration | |url-access=registration | ||
| + | }}</ref> | ||
| + | <ref name=1987PEH> | ||
| + | {{cite book | ||
| + | |last1= Beggs |first1=H. Dale | ||
| + | |title=Oil System Correlations (1987 PEH Chapter 22) | ||
| + | |date=1987 | ||
| + | |publisher=Society of Petroleum Engineers | ||
| + | |url=https://www.onepetro.org/book/peh/spe-1987-22-peh | ||
| + | |url-access=registration | ||
}}</ref> | }}</ref> | ||
</references> | </references> | ||
| Line 67: | Line 121: | ||
[[Category:pengtools]] | [[Category:pengtools]] | ||
[[Category:PVT]] | [[Category:PVT]] | ||
| + | |||
| + | {{#seo: | ||
| + | |title=Beggs and Robinson oil viscosity correlation | ||
| + | |titlemode= replace | ||
| + | |keywords=oil viscosity, Beggs and Robinson correlation, dead oil viscosity | ||
| + | |description=Beggs and Robinson correlation is an empirical correlation for the oil viscosity published in 1975. | ||
| + | }} | ||
Latest revision as of 12:15, 28 September 2020
Contents
Beggs and Robinson Oil Viscosity correlation
Beggs and Robinson is an empirical correlation for the oil viscosity published in 1975 [1].
Math & Physics
Dead oil viscosity:
where:
Saturated oil viscosity (P < Pb):
where:
Undersaturated oil viscosity (P > Pb):
where:
Example. Calculation of the oil viscosity
Example source [3]
Input data
 = 137 F°
= 137 F°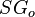 = 0.922 or 22 API
= 0.922 or 22 API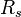 = 90 scf/stb
= 90 scf/stb
Calculate the saturated oil viscosity?
Solution
x = 1.2658
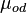 = 17.44 cP
= 17.44 cP
A = 0.719 B = 0.853
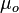 = 8.24 cP
= 8.24 cP
The solution is available in the online PVT calculator software model at www.pengtools.com
Application range
Description of the Data Used[1]:
Number of oil systems = 600
Number of dead oil observations = 460
Number of live oil observations = 2,073
Nomenclature
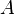 = coefficient
= coefficient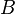 = coefficient
= coefficient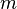 = coefficient
= coefficient = pressure, psia
= pressure, psia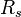 = solution gas-oil ratio, scf/stb
= solution gas-oil ratio, scf/stb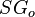 = oil specific gravity, dimensionless
= oil specific gravity, dimensionless = temperature, °F
= temperature, °F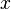 = coefficient
= coefficient
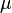 = viscosity, cP
= viscosity, cP
Subscripts
- b - bubble point
- od - dead oil
- os - saturated oil
- o - undersaturated oil
References
- ↑ 1.0 1.1 Beggs, H. D.; Robinson, J. R. (September 1975). "Estimating the Viscosity of Crude Oil Systems"
 . Journal of Petroleum Technology. 27(09) (SPE-5434-PA).
. Journal of Petroleum Technology. 27(09) (SPE-5434-PA).
- ↑
Vasquez, M.; Beggs, H.D. (1980). "Correlations for Fluid Physical Property Prediction."
 . Society of Petroleum Engineers (SPE-6719-PA).
. Society of Petroleum Engineers (SPE-6719-PA).
- ↑
Beggs, H. Dale (1987). Oil System Correlations (1987 PEH Chapter 22)
 . Society of Petroleum Engineers.
. Society of Petroleum Engineers.