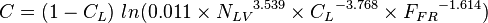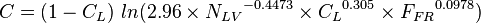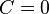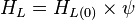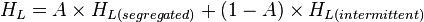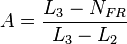Difference between revisions of "Beggs and Brill correlation"
| (3 intermediate revisions by the same user not shown) | |||
| Line 196: | Line 196: | ||
<ref name=BB1991>{{cite book | <ref name=BB1991>{{cite book | ||
| − | |last1= Brill | | + | |last1= Brill |first1=J. P. |
| − | |last2=Beggs| | + | |last2=Beggs|first2=H. D. |
|title=Two-Phase Flow In Pipes | |title=Two-Phase Flow In Pipes | ||
|edition=6 | |edition=6 | ||
| Line 246: | Line 246: | ||
[[Category:pengtools]] | [[Category:pengtools]] | ||
[[Category:sPipe]] | [[Category:sPipe]] | ||
| + | |||
| + | |||
| + | {{#seo: | ||
| + | |title=Beggs and Brill correlation | ||
| + | |titlemode= replace | ||
| + | |keywords=brill wiki, Beggs and Brill, correlation, equation, pipe pressure drop, pipeline sizing, flow rate, fluids flow, Reynolds number, liquid hold up | ||
| + | |description=Beggs and Brill correlation used in pressure drop pipe calculator for pipeline sizing | ||
| + | }} | ||
Latest revision as of 18:10, 3 November 2018
Contents
Brief
Beggs and Brill is an empirical two-phase flow correlation published in 1972 [1].
It distinguish between 4 flow regimes.
Beggs and Brill is the default VLP correlation in sPipe.
Math & Physics
Fluid flow energy balance
where
Friction factor
No slip Reynolds two phase number:
Colebrook–White [3] equation for the Darcy's friction factor:
Corrected two phase friction factor:
where
and
with constraint:
Discussion
Why Beggs and Brill?
The best correlation for the horizontal flow.— pengtools.com
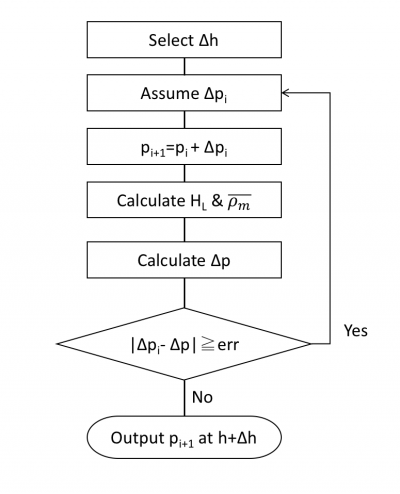
Flow Diagram
Workflow HL
Determine the flow pattern:
Calculate 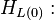
- with the constraint
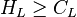 [2]
[2]
C Uphill:
C Downhill:
- ALL:
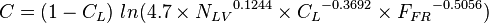 [2]
[2]
- with the restriction
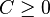 [2]
[2]
Finally:
- SEGREGATED, INTERMITTENT, DISTRIBUTED:
- TRANSITION:
where:
Modifications
1. Force approach gas at low CL. If CL<0.001 Then f'=f.
2. Force approach to single phase fluid. If HL>1 Then HL=1.
3. Use calculated water density instead of the constant value of 62.4 lbm/ft3.
Nomenclature
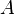 = correlation variable, dimensionless
= correlation variable, dimensionless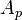 = flow area, ft2
= flow area, ft2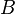 = formation factor, bbl/stb
= formation factor, bbl/stb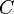 = correlation variable, dimensionless
= correlation variable, dimensionless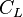 = non-slip liquid holdup factor, dimensionless
= non-slip liquid holdup factor, dimensionless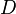 = pipe diameter, ft
= pipe diameter, ft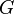 = total flux weight, lbm/ft2/sec
= total flux weight, lbm/ft2/sec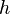 = depth, ft
= depth, ft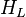 = liquid holdup factor, dimensionless
= liquid holdup factor, dimensionless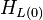 = liquid holdup factor when flow is horizontal, dimensionless
= liquid holdup factor when flow is horizontal, dimensionless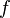 = friction factor, dimensionless
= friction factor, dimensionless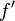 = corrected friction factor, dimensionless
= corrected friction factor, dimensionless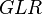 = gas-liquid ratio, scf/bbl
= gas-liquid ratio, scf/bbl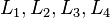 = correlation variables, dimensionless
= correlation variables, dimensionless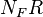 = Froude number, dimensionless
= Froude number, dimensionless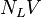 = liquid velocity number, dimensionless
= liquid velocity number, dimensionless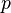 = pressure, psia
= pressure, psia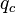 = conversion constant equal to 32.174049, lbmft / lbfsec2
= conversion constant equal to 32.174049, lbmft / lbfsec2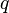 = flow rate, bbl/d - liquid, scf/d - gas
= flow rate, bbl/d - liquid, scf/d - gas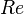 = Reynolds number, dimensionless
= Reynolds number, dimensionless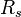 = solution gas-oil ratio, scf/stb
= solution gas-oil ratio, scf/stb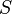 = correlation variable, dimensionless
= correlation variable, dimensionless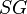 = specific gravity, dimensionless
= specific gravity, dimensionless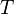 = temperature, °R or °K, follow the subscript
= temperature, °R or °K, follow the subscript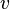 = velocity, ft/sec
= velocity, ft/sec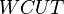 = watercut, fraction
= watercut, fraction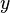 = correlation variable, dimensionless
= correlation variable, dimensionless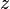 = gas compressibility factor, dimensionless
= gas compressibility factor, dimensionless
Greek symbols
 = absolute roughness, ft
= absolute roughness, ft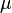 = viscosity, cp
= viscosity, cp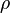 = density, lbm/ft3
= density, lbm/ft3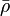 = integrated average density at flowing conditions, lbm/ft3
= integrated average density at flowing conditions, lbm/ft3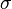 = surface tension of liquid-air interface, dynes/cm (ref. values: 72 - water, 35 - oil)
= surface tension of liquid-air interface, dynes/cm (ref. values: 72 - water, 35 - oil)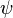 = inclination correction factor, dimensionless
= inclination correction factor, dimensionless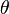 = inclination angle, ° from horizontal
= inclination angle, ° from horizontal
Subscripts
g = gas
K = °K
L = liquid
m = gas/liquid mixture
ns = non-slip
o = oil
R = °R
SL = superficial liquid
SG = superficial gas
w = water
References
- ↑ 1.0 1.1 1.2 1.3 Beggs, H. D.; Brill, J. P. (May 1973). "A Study of Two-Phase Flow in Inclined Pipes"
 . Journal of Petroleum Technology. AIME. 255 (SPE-4007-PA).
. Journal of Petroleum Technology. AIME. 255 (SPE-4007-PA).
- ↑ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 2.13 2.14 2.15 2.16 2.17 2.18 2.19 2.20 2.21 2.22 2.23 2.24 2.25 2.26 Brill, J. P.; Beggs, H. D. (1991). Two-Phase Flow In Pipes
 (6 ed.). Oklahoma: U. of Tulsa Tulsa.
(6 ed.). Oklahoma: U. of Tulsa Tulsa.
- ↑ Colebrook, C. F. (1938–1939). "Turbulent Flow in Pipes, With Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws"
 . Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
. Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
- ↑ Moody, L. F. (1944). "Friction factors for pipe flow"
 . Transactions of the ASME. 66 (8): 671–684.
. Transactions of the ASME. 66 (8): 671–684.
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 5.6 Lyons, W.C. (1996). Standard handbook of petroleum and natural gas engineering. 2. Houston, TX: Gulf Professional Publishing. ISBN 0-88415-643-5.
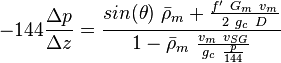
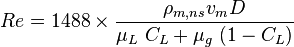
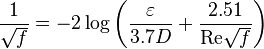
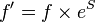
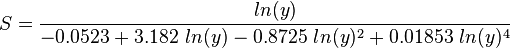
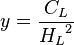
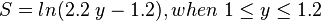
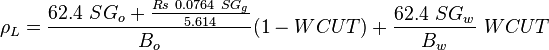
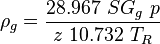
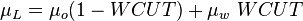
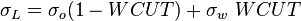
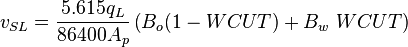
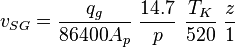
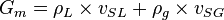
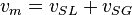
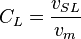
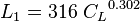
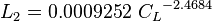
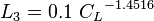
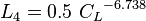
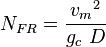
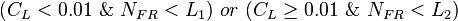
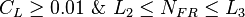
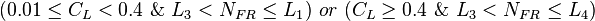
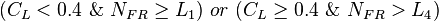
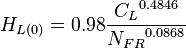
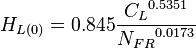
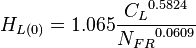
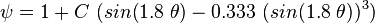
![N_{LV} = 1.938\ v_{SL}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}}](/images/math/d/d/8/dd824df0b6ec22aa724161b929e993fe.png)