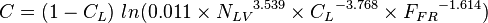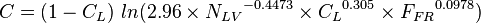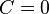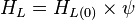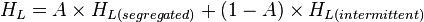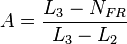Difference between revisions of "Beggs and Brill correlation"
(→Workflow HL) |
|||
| (38 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
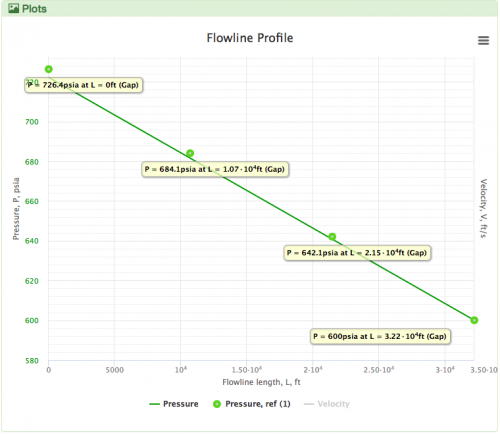
[[Beggs and Brill correlation |Beggs and Brill]] is the default [[VLP]] correlation in [[:Category:sPipe|sPipe]]. | [[Beggs and Brill correlation |Beggs and Brill]] is the default [[VLP]] correlation in [[:Category:sPipe|sPipe]]. | ||
| − | [[File: Beggs and Brill.png|thumb|500px|link=https://www.pengtools.com|Beggs and Brill in sPipe Vs GAP |right]] | + | [[File: Beggs and Brill.png|thumb|500px|link=https://www.pengtools.com/sPipe?paramsToken=cc8af4bdd85a3d7da86119d5367742e2|Beggs and Brill in sPipe Vs GAP |right]] |
== Math & Physics == | == Math & Physics == | ||
=== Fluid flow energy balance === | === Fluid flow energy balance === | ||
| − | :<math> -144 \frac{\Delta p}{\Delta z} = \frac{sin(\theta)\ \bar \rho_m + \frac{f'\ G_m\ v_m}{2\ g_c\ D}}{1- \bar \rho_m\ \frac{v_m\ v_{SG}}{g_c\ p}}</math><ref name="BB" /> | + | :<math> -144 \frac{\Delta p}{\Delta z} = \frac{sin(\theta)\ \bar \rho_m + \frac{f'\ G_m\ v_m}{2\ g_c\ D}}{1- \bar \rho_m\ \frac{v_m\ v_{SG}}{g_c\ \frac{p}{144}}}</math><ref name="BB" /> |
where | where | ||
:<math> \bar \rho_m = \rho_L H_L + \rho_g (1 - H_L)</math><ref name="BB" /> | :<math> \bar \rho_m = \rho_L H_L + \rho_g (1 - H_L)</math><ref name="BB" /> | ||
| Line 17: | Line 17: | ||
=== Friction factor === | === Friction factor === | ||
No slip Reynolds two phase number: | No slip Reynolds two phase number: | ||
| − | :<math> Re = 1488 \times \frac {\rho_{m,ns} v_m D} | + | :<math> Re = 1488 \times \frac {\rho_{m,ns} v_m D} { \mu_L\ C_L + \mu_g\ (1-C_L) } </math><ref name="BB1991" /> |
Colebrook–White <ref name=Colebrook/> equation for the [http://en.wikipedia.org/wiki/Darcy_friction_factor_formulae Darcy's friction factor]: | Colebrook–White <ref name=Colebrook/> equation for the [http://en.wikipedia.org/wiki/Darcy_friction_factor_formulae Darcy's friction factor]: | ||
| Line 27: | Line 27: | ||
where | where | ||
| − | :<math> S = \frac{ ln(y)}{ -0.0523 + 3.182\ ln(y) - 0.8725\ ln(y)^2 + 0.01853\ ln(y)^ 4}</math><ref name="BB1991" /> | + | :<math> S = \frac{ ln(y)}{ -0.0523 + 3.182\ ln(y) - 0.8725\ ln(y)^{2} + 0.01853\ ln(y)^{4}}</math><ref name="BB1991" /> |
and | and | ||
| Line 34: | Line 34: | ||
with constraint: | with constraint: | ||
| − | :<math> S = ln (2.2\ y - 1.2), when\ 1 | + | :<math> S = ln (2.2\ y - 1.2), when\ 1 \le y \le 1.2 </math><ref name="BB1991" /> |
== Discussion == | == Discussion == | ||
| − | Why [[ | + | Why [[Beggs and Brill correlation| Beggs and Brill]]? |
| − | {{Quote| text = | + | {{Quote| text = The best correlation for the horizontal flow. | source = pengtools.com}} |
== Flow Diagram == | == Flow Diagram == | ||
| Line 71: | Line 71: | ||
:<math> L_4 = 0.5\ {C_L}^{-6.738}</math><ref name= BB1991/> | :<math> L_4 = 0.5\ {C_L}^{-6.738}</math><ref name= BB1991/> | ||
| − | <math> N_{FR} = \frac{{v_m}^2}{g_c\ D}</math><ref name="BB" /> | + | :<math> N_{FR} = \frac{{v_m}^2}{g_c\ D}</math><ref name="BB" /> |
| − | Determine the flow pattern: | + | '''Determine the flow pattern:''' |
| − | SEGREGATED: <math> (C_L < 0.01\ \&\ N_{FR}< L_1)\ or\ (C_L\ge0.01\ \&\ N_{FR}<L_2)</math><ref name="BB1991" /> | + | *SEGREGATED: <math> (C_L < 0.01\ \&\ N_{FR}< L_1)\ or\ (C_L\ge0.01\ \&\ N_{FR}<L_2)</math><ref name="BB1991" /> |
| + | *TRANSITION: <math> C_L \ge 0.01\ \&\ L_2 \le N_{FR} \le L_3</math><ref name="BB1991" /> | ||
| + | *INTERMITTENT: <math> (0.01 \le C_L <0.4\ \&\ L_3<N_{FR}\le L_1)\ or\ ( C_L\ge0.4\ \&\ L_3<N_{FR} \le L_4)</math><ref name="BB1991" /> | ||
| + | *DISTRIBUTED: <math> (C_L < 0.4\ \&\ N_{FR} \ge L_1)\ or\ (C_L\ge0.4\ \&\ N_{FR}>L_4)</math><ref name="BB1991" /> | ||
| − | + | '''Calculate <math> H_{L(0)}:</math>''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <math> H_{L(0)}:</math> | ||
*SEGREGATED: <math> H_{L(0)} = 0.98 \frac{ {C_L}^{0.4846} } { {N_{FR}}^{0.0868}} </math><ref name="BB1991" /> | *SEGREGATED: <math> H_{L(0)} = 0.98 \frac{ {C_L}^{0.4846} } { {N_{FR}}^{0.0868}} </math><ref name="BB1991" /> | ||
*INTERMITTENT: <math> H_{L(0)} = 0.845 \frac{ {C_L}^{0.5351} } { {N_{FR}}^{0.0173}}</math><ref name="BB1991" /> | *INTERMITTENT: <math> H_{L(0)} = 0.845 \frac{ {C_L}^{0.5351} } { {N_{FR}}^{0.0173}}</math><ref name="BB1991" /> | ||
*DISTRIBUTED: <math> H_{L(0)} = 1.065\frac{ {C_L}^{0.5824} } { {N_{FR}}^{0.0609}}</math><ref name="BB1991" /> | *DISTRIBUTED: <math> H_{L(0)} = 1.065\frac{ {C_L}^{0.5824} } { {N_{FR}}^{0.0609}}</math><ref name="BB1991" /> | ||
| − | with the constraint <math> H_L \ge C_L</math><ref name="BB1991" /> | + | :with the constraint <math> H_L \ge C_L</math><ref name="BB1991" /> |
| + | |||
:<math> \psi = 1 + C\ (sin(1.8\ \theta) - 0.333\ (sin(1.8\ \theta))^3)</math><ref name="BB1991" /> | :<math> \psi = 1 + C\ (sin(1.8\ \theta) - 0.333\ (sin(1.8\ \theta))^3)</math><ref name="BB1991" /> | ||
| − | :<math> N_{LV} = 1.938\ v_{SL}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}} </math><ref name= | + | :<math> N_{LV} = 1.938\ v_{SL}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}} </math><ref name= BB1991/> |
'''C Uphill:''' | '''C Uphill:''' | ||
| Line 102: | Line 100: | ||
*ALL: <math> C = (1-C_L)\ ln( 4.7\times {N_{LV}}^{0.1244}\times {C_L}^{-0.3692}\times {F_{FR}}^{-0.5056})</math><ref name="BB1991" /> | *ALL: <math> C = (1-C_L)\ ln( 4.7\times {N_{LV}}^{0.1244}\times {C_L}^{-0.3692}\times {F_{FR}}^{-0.5056})</math><ref name="BB1991" /> | ||
| − | with the restriction <math> C \ge 0 </math><ref name="BB1991" /> | + | :with the restriction <math> C \ge 0 </math><ref name="BB1991" /> |
| − | + | '''Finally:''' | |
| − | + | *SEGREGATED, INTERMITTENT, DISTRIBUTED: | |
| − | + | :<math> H_L = H_{L(0)} \times \psi </math><ref name="BB1991" /> | |
| − | <math> H_L = A \times H_{L(segregated)} + (1-A) \times {H_{L(intermittent)}} </math><ref name="BB1991" /> | + | *TRANSITION: |
| + | |||
| + | :<math> H_L = A \times H_{L(segregated)} + (1-A) \times {H_{L(intermittent)}} </math><ref name="BB1991" /> | ||
where: | where: | ||
| − | <math> A = \frac{L_3-N_{FR}}{L_3-L_2}</math><ref name="BB1991" | + | :<math> A = \frac{L_3-N_{FR}}{L_3-L_2}</math><ref name="BB1991" /> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Modifications == | == Modifications == | ||
| − | 1. | + | 1. Force approach gas at low C<sub>L</sub>. If C<sub>L</sub><0.001 Then f'=f. |
| − | 2. | + | 2. Force approach to single phase fluid. If H<sub>L</sub>>1 Then H<sub>L</sub>=1. |
| − | 3. Use | + | 3. Use calculated water density instead of the constant value of 62.4 lbm/ft3. |
== Nomenclature == | == Nomenclature == | ||
| + | :<math> A </math> = correlation variable, dimensionless | ||
:<math> A_p </math> = flow area, ft2 | :<math> A_p </math> = flow area, ft2 | ||
| − | |||
:<math> B </math> = formation factor, bbl/stb | :<math> B </math> = formation factor, bbl/stb | ||
| − | :<math> C </math> = | + | :<math> C </math> = correlation variable, dimensionless |
| + | :<math> C_L </math> = non-slip liquid holdup factor, dimensionless | ||
:<math> D </math> = pipe diameter, ft | :<math> D </math> = pipe diameter, ft | ||
| + | :<math> G </math> = total flux weight, lb<sub>m</sub>/ft<sup>2</sup>/sec | ||
:<math> h </math> = depth, ft | :<math> h </math> = depth, ft | ||
| − | |||
:<math> H_L </math> = liquid holdup factor, dimensionless | :<math> H_L </math> = liquid holdup factor, dimensionless | ||
| + | :<math> H_{L(0)} </math> = liquid holdup factor when flow is horizontal, dimensionless | ||
:<math> f </math> = friction factor, dimensionless | :<math> f </math> = friction factor, dimensionless | ||
| + | :<math> f' </math> = corrected friction factor, dimensionless | ||
:<math> GLR </math> = gas-liquid ratio, scf/bbl | :<math> GLR </math> = gas-liquid ratio, scf/bbl | ||
| − | :<math> | + | :<math> L_1, L_2, L_3, L_4 </math> = correlation variables, dimensionless |
| − | + | :<math> N_FR </math> = Froude number, dimensionless | |
| − | |||
| − | :<math> | ||
:<math> N_LV </math> = liquid velocity number, dimensionless | :<math> N_LV </math> = liquid velocity number, dimensionless | ||
:<math> p </math> = pressure, psia | :<math> p </math> = pressure, psia | ||
:<math> q_c </math> = conversion constant equal to 32.174049, lb<sub>m</sub>ft / lb<sub>f</sub>sec<sup>2</sup> | :<math> q_c </math> = conversion constant equal to 32.174049, lb<sub>m</sub>ft / lb<sub>f</sub>sec<sup>2</sup> | ||
| − | :<math> q </math> = | + | :<math> q </math> = flow rate, bbl/d - liquid, scf/d - gas |
:<math> Re </math> = Reynolds number, dimensionless | :<math> Re </math> = Reynolds number, dimensionless | ||
:<math> R_s </math> = solution gas-oil ratio, scf/stb | :<math> R_s </math> = solution gas-oil ratio, scf/stb | ||
| + | :<math> S </math> = correlation variable, dimensionless | ||
:<math> SG </math> = specific gravity, dimensionless | :<math> SG </math> = specific gravity, dimensionless | ||
:<math> T </math> = temperature, °R or °K, follow the subscript | :<math> T </math> = temperature, °R or °K, follow the subscript | ||
:<math> v </math> = velocity, ft/sec | :<math> v </math> = velocity, ft/sec | ||
| − | :<math> | + | :<math> WCUT </math> = watercut, fraction |
| + | :<math> y </math> = correlation variable, dimensionless | ||
:<math> z </math> = gas compressibility factor, dimensionless | :<math> z </math> = gas compressibility factor, dimensionless | ||
| Line 182: | Line 159: | ||
:<math> \mu </math> = viscosity, cp | :<math> \mu </math> = viscosity, cp | ||
:<math> \rho </math> = density, lb<sub>m</sub>/ft<sup>3</sup> | :<math> \rho </math> = density, lb<sub>m</sub>/ft<sup>3</sup> | ||
| − | :<math> \bar \rho </math> = integrated average density at flowing conditions, lb<sub>m</sub>/ft<sup> | + | :<math> \bar \rho </math> = integrated average density at flowing conditions, lb<sub>m</sub>/ft<sup>3</sup> |
:<math> \sigma </math> = surface tension of liquid-air interface, dynes/cm (ref. values: 72 - water, 35 - oil) | :<math> \sigma </math> = surface tension of liquid-air interface, dynes/cm (ref. values: 72 - water, 35 - oil) | ||
| − | :<math> \psi </math> = | + | :<math> \psi </math> = inclination correction factor, dimensionless |
| + | :<math> \theta </math> = inclination angle, ° from horizontal | ||
===Subscripts=== | ===Subscripts=== | ||
| Line 192: | Line 170: | ||
L = liquid<BR/> | L = liquid<BR/> | ||
m = gas/liquid mixture<BR/> | m = gas/liquid mixture<BR/> | ||
| + | ns = non-slip<BR/> | ||
o = oil<BR/> | o = oil<BR/> | ||
R = °R<BR/> | R = °R<BR/> | ||
| Line 216: | Line 195: | ||
}}</ref> | }}</ref> | ||
| − | <ref name= | + | <ref name=BB1991>{{cite book |
| − | |last1= | + | |last1= Brill |first1=J. P. |
| − | |last2= | + | |last2=Beggs|first2=H. D. |
| − | + | |title=Two-Phase Flow In Pipes | |
| − | + | |edition=6 | |
| − | |title= | + | |date=1991 |
| − | |edition= | + | |publisher=U. of Tulsa Tulsa |
| − | |date= | + | |place=Oklahoma |
| − | |publisher= | + | |url=https://www.scribd.com/document/130564301/Twophase-Flow-in-Pipes-Beggs-Amp-Brill |
| − | |place= | + | |url-access=subscription |
| − | | | ||
}}</ref> | }}</ref> | ||
| Line 262: | Line 240: | ||
|place=Houston, TX | |place=Houston, TX | ||
|isbn=0-88415-643-5 | |isbn=0-88415-643-5 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}}</ref> | }}</ref> | ||
| Line 276: | Line 245: | ||
[[Category:pengtools]] | [[Category:pengtools]] | ||
| − | [[Category: | + | [[Category:sPipe]] |
| + | |||
| + | |||
| + | {{#seo: | ||
| + | |title=Beggs and Brill correlation | ||
| + | |titlemode= replace | ||
| + | |keywords=brill wiki, Beggs and Brill, correlation, equation, pipe pressure drop, pipeline sizing, flow rate, fluids flow, Reynolds number, liquid hold up | ||
| + | |description=Beggs and Brill correlation used in pressure drop pipe calculator for pipeline sizing | ||
| + | }} | ||
Latest revision as of 18:10, 3 November 2018
Contents
Brief
Beggs and Brill is an empirical two-phase flow correlation published in 1972 [1].
It distinguish between 4 flow regimes.
Beggs and Brill is the default VLP correlation in sPipe.
Math & Physics
Fluid flow energy balance
where
Friction factor
No slip Reynolds two phase number:
Colebrook–White [3] equation for the Darcy's friction factor:
Corrected two phase friction factor:
where
and
with constraint:
Discussion
Why Beggs and Brill?
The best correlation for the horizontal flow.— pengtools.com
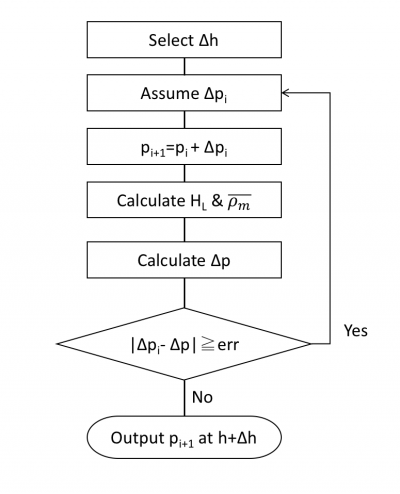
Flow Diagram
Workflow HL
Determine the flow pattern:
Calculate 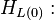
- with the constraint
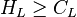 [2]
[2]
C Uphill:
C Downhill:
- ALL:
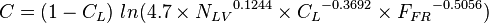 [2]
[2]
- with the restriction
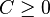 [2]
[2]
Finally:
- SEGREGATED, INTERMITTENT, DISTRIBUTED:
- TRANSITION:
where:
Modifications
1. Force approach gas at low CL. If CL<0.001 Then f'=f.
2. Force approach to single phase fluid. If HL>1 Then HL=1.
3. Use calculated water density instead of the constant value of 62.4 lbm/ft3.
Nomenclature
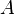 = correlation variable, dimensionless
= correlation variable, dimensionless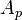 = flow area, ft2
= flow area, ft2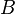 = formation factor, bbl/stb
= formation factor, bbl/stb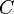 = correlation variable, dimensionless
= correlation variable, dimensionless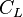 = non-slip liquid holdup factor, dimensionless
= non-slip liquid holdup factor, dimensionless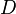 = pipe diameter, ft
= pipe diameter, ft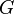 = total flux weight, lbm/ft2/sec
= total flux weight, lbm/ft2/sec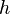 = depth, ft
= depth, ft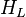 = liquid holdup factor, dimensionless
= liquid holdup factor, dimensionless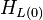 = liquid holdup factor when flow is horizontal, dimensionless
= liquid holdup factor when flow is horizontal, dimensionless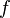 = friction factor, dimensionless
= friction factor, dimensionless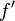 = corrected friction factor, dimensionless
= corrected friction factor, dimensionless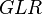 = gas-liquid ratio, scf/bbl
= gas-liquid ratio, scf/bbl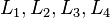 = correlation variables, dimensionless
= correlation variables, dimensionless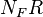 = Froude number, dimensionless
= Froude number, dimensionless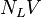 = liquid velocity number, dimensionless
= liquid velocity number, dimensionless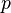 = pressure, psia
= pressure, psia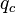 = conversion constant equal to 32.174049, lbmft / lbfsec2
= conversion constant equal to 32.174049, lbmft / lbfsec2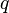 = flow rate, bbl/d - liquid, scf/d - gas
= flow rate, bbl/d - liquid, scf/d - gas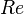 = Reynolds number, dimensionless
= Reynolds number, dimensionless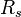 = solution gas-oil ratio, scf/stb
= solution gas-oil ratio, scf/stb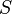 = correlation variable, dimensionless
= correlation variable, dimensionless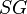 = specific gravity, dimensionless
= specific gravity, dimensionless = temperature, °R or °K, follow the subscript
= temperature, °R or °K, follow the subscript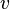 = velocity, ft/sec
= velocity, ft/sec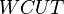 = watercut, fraction
= watercut, fraction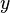 = correlation variable, dimensionless
= correlation variable, dimensionless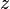 = gas compressibility factor, dimensionless
= gas compressibility factor, dimensionless
Greek symbols
 = absolute roughness, ft
= absolute roughness, ft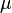 = viscosity, cp
= viscosity, cp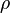 = density, lbm/ft3
= density, lbm/ft3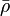 = integrated average density at flowing conditions, lbm/ft3
= integrated average density at flowing conditions, lbm/ft3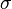 = surface tension of liquid-air interface, dynes/cm (ref. values: 72 - water, 35 - oil)
= surface tension of liquid-air interface, dynes/cm (ref. values: 72 - water, 35 - oil)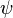 = inclination correction factor, dimensionless
= inclination correction factor, dimensionless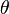 = inclination angle, ° from horizontal
= inclination angle, ° from horizontal
Subscripts
g = gas
K = °K
L = liquid
m = gas/liquid mixture
ns = non-slip
o = oil
R = °R
SL = superficial liquid
SG = superficial gas
w = water
References
- ↑ 1.0 1.1 1.2 1.3 Beggs, H. D.; Brill, J. P. (May 1973). "A Study of Two-Phase Flow in Inclined Pipes"
 . Journal of Petroleum Technology. AIME. 255 (SPE-4007-PA).
. Journal of Petroleum Technology. AIME. 255 (SPE-4007-PA).
- ↑ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 2.13 2.14 2.15 2.16 2.17 2.18 2.19 2.20 2.21 2.22 2.23 2.24 2.25 2.26 Brill, J. P.; Beggs, H. D. (1991). Two-Phase Flow In Pipes
 (6 ed.). Oklahoma: U. of Tulsa Tulsa.
(6 ed.). Oklahoma: U. of Tulsa Tulsa.
- ↑ Colebrook, C. F. (1938–1939). "Turbulent Flow in Pipes, With Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws"
 . Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
. Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
- ↑ Moody, L. F. (1944). "Friction factors for pipe flow"
 . Transactions of the ASME. 66 (8): 671–684.
. Transactions of the ASME. 66 (8): 671–684.
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 5.6 Lyons, W.C. (1996). Standard handbook of petroleum and natural gas engineering. 2. Houston, TX: Gulf Professional Publishing. ISBN 0-88415-643-5.
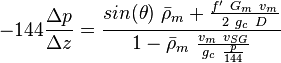
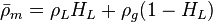
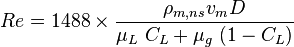
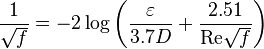
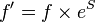
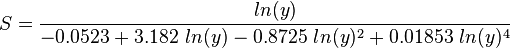
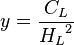
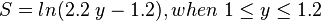
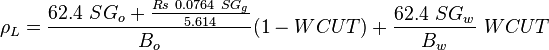
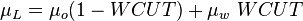
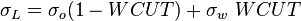
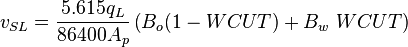
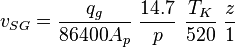
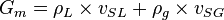
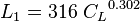
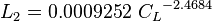
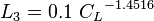
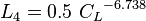
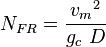
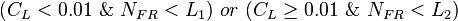
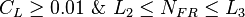
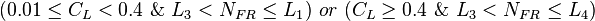
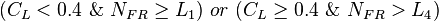
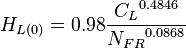
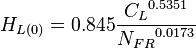
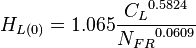
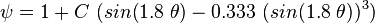
![N_{LV} = 1.938\ v_{SL}\ \sqrt[4]{\frac{\rho_L}{\sigma_L}}](/images/math/d/d/8/dd824df0b6ec22aa724161b929e993fe.png)