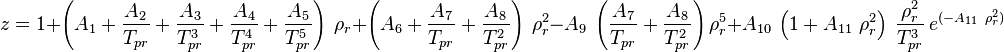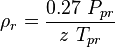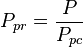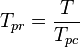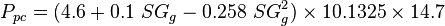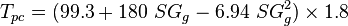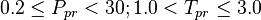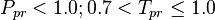Difference between revisions of "Dranchuk correlation"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Math & Physics)
 
(46 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 
__TOC__
 
__TOC__
  
−
=== Brief ===
+
== Dranchuk gas compressibility factor correlation ==
  
−
[[Dranchuk correlation]] is the fitting function of the classic '''Standing and Katz''' <ref name=Standing&Katz /> gas compressibility factor correlation.
+
[[Dranchuk correlation]] is the fitting equation of the classic '''Standing and Katz''' <ref name=Standing&Katz /> [[gas compressibility factor]] correlation.
  
−
=== Math & Physics ===
+
== Math & Physics ==
−
A1 = 0.3265<br/>
+
:<math> z =  1 +
−
A2 = –1.0700<br/>
 
−
A3 = –0.5339<br/>
 
−
A4 = 0.01569<br/>
 
−
A5 = –0.05165<br/>
 
−
A6 = 0.5475<br/>
 
−
A7 = –0.7361<br/>
 
−
A8 = 0.1844<br/>
 
−
A9 = 0.1056<br/>
 
−
A10 = 0.6134<br/>
 
−
A11 = 0.7210<br/>
 
−
:<math> z =  1-z+
 
 
\left(A_1
 
\left(A_1
 
  +\frac{A_2}{T_{pr}}
 
  +\frac{A_2}{T_{pr}}
Line 28: Line 17:
 
  +\frac{A_8}{T^2_{pr}}
 
  +\frac{A_8}{T^2_{pr}}
 
\right)\ \rho^2_r
 
\right)\ \rho^2_r
−
-A_9\ \left(\frac{A_7}{T_{pr}}+\frac{A_8}{T^2_{pr}}\right)
+
-A_9\ \left(\frac{A_7}{T_{pr}}+\frac{A_8}{T^2_{pr}}\right) \rho^5_r
 
+A_{10}\ \left(1+A_{11}\ \rho^2_r\right)\ \frac{\rho^2_r}{T^3_{pr}}
 
+A_{10}\ \left(1+A_{11}\ \rho^2_r\right)\ \frac{\rho^2_r}{T^3_{pr}}
−
\ e^{-A_{11}\ \rho^2_r}
+
\ e^{(-A_{11}\ \rho^2_r)}
 
</math><ref name= Dranchuk/>
 
</math><ref name= Dranchuk/>
−
where
 
−
:<math>  T_{pc} =  99.3+180\ SG_g-6.94\ SG^2_g</math>
 
  
−
:<math>  P_{pc} =  4.6+0.1\ SG_g-0.258\ SG^2_g</math>
+
where:
 +
 
 +
:<math>  \rho_r = \frac{0.27\ P_{pr}}{{z\ T_{pr}}}  </math>
 +
 
 +
:<math>  P_{pr} =  \frac{P}{P_{pc}}</math>
  
 
:<math>  T_{pr} =  \frac{T}{T_{pc}}</math>
 
:<math>  T_{pr} =  \frac{T}{T_{pc}}</math>
  
−
:<math>  P_{pr} =  \frac{P}{P_{pc}}</math>
 
  
−
:<math>  \rho_r = \frac{0.27\ P_{pr}}{({z\ T_{pr}})}  </math>
+
A1 = 0.3265<br/>
 +
A2 = –1.0700<br/>
 +
A3 = –0.5339<br/>
 +
A4 = 0.01569<br/>
 +
A5 = –0.05165<br/>
 +
A6 = 0.5475<br/>
 +
A7 = –0.7361<br/>
 +
A8 = 0.1844<br/>
 +
A9 = 0.1056<br/>
 +
A10 = 0.6134<br/>
 +
A11 = 0.7210<br/>
 +
 
 +
== Discussion ==
 +
Why the [[Dranchuk correlation]]?
 +
 
 +
{{Quote| text = It's classics! | source = www.pengtools.com}}
 +
 
 +
== Workflow  ==
 +
To solve the [[Dranchuk correlation| Dranchuk]] equation use the iterative secant method.
 +
 
 +
To find the pseudo critical properties from the gas specific gravity <ref name=Standing&Katz />:
 +
 
 +
:<math>  P_{pc} =  ( 4.6+0.1\ SG_g-0.258\ SG^2_g ) \times 10.1325 \times 14.7</math>
  
−
=== Discussion ===
+
:<math>  T_{pc} =  ( 99.3+180\ SG_g-6.94\ SG^2_g ) \times 1.8 </math>
−
To avoid the [[Liquid loading]] the gas velocity should be above the [[Liquid loading]] velocity.
 
  
−
The higher the gas rate the higher the gas velocity.
+
== Application range ==
  
−
The lower the wellhead flowing pressure the higher the gas rate.
+
:<math>  0.2 \le P_{pr} < 30 ; 1.0 < T_{pr} \le 3.0 </math><ref name= Dranchuk/>
  
−
The bigger the tubing ID the higher the gas rate.
+
and
  
−
In case when the gas rate is limited by the [[Reservoirs|Reservoir]] deliverability smaller tubing ID will increase the gas velocity.
+
:<math>  P_{pr} < 1.0 ; 0.7 < T_{pr} \le 1.0</math><ref name= Dranchuk/>
  
−
=== Nomenclature ===
+
== Nomenclature ==
−
:<math> A_1..A_{11} </math> coefficients
+
:<math> A_1..A_{11} </math> = coefficients
 
:<math> \rho_r </math> = reduced density, dimensionless
 
:<math> \rho_r </math> = reduced density, dimensionless
−
:<math> P </math> = Pressure, psia
+
:<math> P </math> = pressure, psia
 
:<math> P_{pc} </math> = pseudo critical pressure, psia
 
:<math> P_{pc} </math> = pseudo critical pressure, psia
 
:<math> P_{pr} </math> = pseudoreduced pressure, dimensionless
 
:<math> P_{pr} </math> = pseudoreduced pressure, dimensionless
−
:<math> SG_g </math> = gas specific density, dimensionless
+
:<math> SG_g </math> = gas specific gravity, dimensionless
 
:<math> T </math> = temperature, °R
 
:<math> T </math> = temperature, °R
 
:<math> T_{pc} </math> = pseudo critical temperature, °R
 
:<math> T_{pc} </math> = pseudo critical temperature, °R
Line 66: Line 77:
 
:<math> z </math> = gas compressibility factor, dimensionless
 
:<math> z </math> = gas compressibility factor, dimensionless
  
−
=== References ===
+
== References ==
 
<references>
 
<references>
  
Line 98: Line 109:
 
[[Category:pengtools]]
 
[[Category:pengtools]]
 
[[Category:PVT]]
 
[[Category:PVT]]
 +
 +
 +
{{#seo:
 +
|title=Dranchuk gas compressibility factor correlation
 +
|titlemode= replace
 +
|keywords=Dranchuk correlation
 +
|description=Dranchuk correlation is the fitting equation of the classic Standing and Katz gas compressibility factor correlation.
 +
}}

Latest revision as of 21:29, 23 November 2023

Dranchuk gas compressibility factor correlation

Dranchuk correlation is the fitting equation of the classic Standing and Katz [1] gas compressibility factor correlation.

Math & Physics

z = 1 + \left(A_1 +\frac{A_2}{T_{pr}} +\frac{A_3}{T^3_{pr}} +\frac{A_4}{T^4_{pr}} +\frac{A_5}{T^5_{pr}} \right)\ \rho_r+ \left(A_6 +\frac{A_7}{T_{pr}} +\frac{A_8}{T^2_{pr}} \right)\ \rho^2_r -A_9\ \left(\frac{A_7}{T_{pr}}+\frac{A_8}{T^2_{pr}}\right) \rho^5_r +A_{10}\ \left(1+A_{11}\ \rho^2_r\right)\ \frac{\rho^2_r}{T^3_{pr}} \ e^{(-A_{11}\ \rho^2_r)} [2]

where:

\rho_r = \frac{0.27\ P_{pr}}{{z\ T_{pr}}}
P_{pr} = \frac{P}{P_{pc}}
T_{pr} = \frac{T}{T_{pc}}


A1 = 0.3265
A2 = –1.0700
A3 = –0.5339
A4 = 0.01569
A5 = –0.05165
A6 = 0.5475
A7 = –0.7361
A8 = 0.1844
A9 = 0.1056
A10 = 0.6134
A11 = 0.7210

Discussion

Why the Dranchuk correlation?

It's classics!
— www.pengtools.com

Workflow

To solve the Dranchuk equation use the iterative secant method.

To find the pseudo critical properties from the gas specific gravity [1]:

P_{pc} = ( 4.6+0.1\ SG_g-0.258\ SG^2_g ) \times 10.1325 \times 14.7
T_{pc} = ( 99.3+180\ SG_g-6.94\ SG^2_g ) \times 1.8

Application range

0.2 \le P_{pr} < 30 ; 1.0 < T_{pr} \le 3.0 [2]

and

P_{pr} < 1.0 ; 0.7 < T_{pr} \le 1.0[2]

Nomenclature

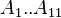A_1..A_{11} = coefficients
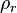\rho_r = reduced density, dimensionless
P = pressure, psia
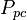P_{pc} = pseudo critical pressure, psia
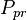P_{pr} = pseudoreduced pressure, dimensionless
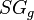SG_g = gas specific gravity, dimensionless
T = temperature, °R
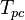T_{pc} = pseudo critical temperature, °R
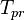T_{pr} = pseudoreduced temperature, dimensionless
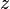z = gas compressibility factor, dimensionless

References

  1. ↑ 1.0 1.1 Standing, M. B.; Katz, D. L. (December 1942). "Density of Natural Gases"Free registration required. Transactions of the AIME. Society of Petroleum Engineers. 146 (SPE-942140-G). 
  2. ↑ 2.0 2.1 2.2 Dranchuk, P. M.; Abou-Kassem, H. (July 1975). "Calculation of Z Factors For Natural Gases Using Equations of State"Free registration required. The Journal of Canadian Petroleum. 14 (PETSOC-75-03-03). 


Retrieved from "https://wiki.pengtools.com/index.php?title=Dranchuk_correlation&oldid=7719"