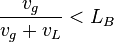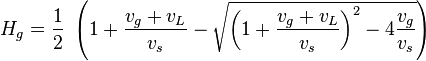Difference between revisions of "Griffith correlation"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Math & Physics)
 
(13 intermediate revisions by the same user not shown)
Line 8: Line 8:
  
 
The bubble flow exist when:
 
The bubble flow exist when:
−
:<math> \frac{v_g}{v_g + v_L} < L_B </math><ref name= Orkiszewski />
+
:<math> \frac{v_g}{v_g + v_L} < L_B </math><ref name= Economides />
  
 
:<math> L_B = 1.071 - 0.2218 \frac{(v_g+v_L)^2}{D}</math>, with the limit <math> L_B \geqslant 0.13 </math><ref name= Orkiszewski />
 
:<math> L_B = 1.071 - 0.2218 \frac{(v_g+v_L)^2}{D}</math>, with the limit <math> L_B \geqslant 0.13 </math><ref name= Orkiszewski />
Line 16: Line 16:
  
 
== Discussion  ==
 
== Discussion  ==
 +
 +
[[Griffith correlation]] adds a hook to the originally straight [[Hagedorn and Brown]] [[VLP]] curve.
 +
 
== Nomenclature  ==
 
== Nomenclature  ==
  
 +
:<math> D </math> = pipe diameter, ft
 
:<math> H_g </math> = gas holdup factor, dimensionless
 
:<math> H_g </math> = gas holdup factor, dimensionless
−
:<math> f </math> = friction factor, dimensionless
+
:<math> L_B </math> = bubble-slug boundary, dimensionless
−
:<math> GLR </math> = gas-liquid ratio, scf/bbl
+
:<math> v_g </math> = gas velocity, ft/sec
−
:<math> M </math> = total mass of oil, water and gas associated with 1 bbl of liquid flowing into and out of the flow string, lb<sub>m</sub>/bbl
+
:<math> v_L </math> = liquid velocity, ft/sec
−
:<math> N_D </math> = pipe diameter number number, dimensionless
+
:<math> v_s </math> = 0.8, slip velocity (difference between average gas and liquid velocities), ft/sec
−
:<math> N_GV </math> = gas velocity number, dimensionless
 
−
:<math> N_L </math> = liquid viscosity number, dimensionless
 
−
:<math> N_LV </math> = liquid velocity number, dimensionless
 
−
:<math> p </math> = pressure, psia
 
−
:<math> q_c </math> = conversion constant equal to 32.174, lb<sub>m</sub>ft / lb<sub>f</sub>sec<sup>2</sup>
 
−
:<math> q_L </math> = total liquid production rate, bbl/d
 
−
:<math> Re </math> = Reynolds number, dimensionless
 
−
:<math> R_s </math> = solution gas-oil ratio, scf/stb
 
−
:<math> SG </math> = specific gravity, dimensionless
 
−
:<math> T </math> = temperature, °R or °K, follow the subscript
 
−
:<math> v </math> = velocity, ft/sec
 
−
:<math> WOR </math> = water-oil ratio, bbl/bbl
 
−
:<math> z </math> = gas compressibility factor, dimensionless
 
  
 
== References ==
 
== References ==
Line 63: Line 54:
 
  |url=https://www.onepetro.org/journal-paper/SPE-1546-PA
 
  |url=https://www.onepetro.org/journal-paper/SPE-1546-PA
 
  |url-access= subscription  
 
  |url-access= subscription  
 +
}}</ref>
 +
 +
<ref name=Economides>{{cite book
 +
|last1= Economides |first1=M.J.
 +
|last2= Hill |first2=A.D.
 +
|last3= Economides |first3=C.E.
 +
|last4= Zhu |first4=D.
 +
|title=Petroleum Production Systems
 +
|edition=2
 +
|date=2013
 +
|publisher=Prentice Hall
 +
|place=Westford, Massachusetts
 +
|isbn=978-0-13-703158-0
 
}}</ref>
 
}}</ref>
 
</references>
 
</references>
  
 
[[Category:pengtools]]
 
[[Category:pengtools]]
−
[[Category:pqPlot]]
+
[[Category:PQplot]]
 +
 
 +
{{#seo:
 +
|title=Griffith correlation
 +
|titlemode= replace
 +
|keywords=Griffith correlation
 +
|description=Griffith correlation is an empirical correlation which defines: the boundary between the bubble and slug flow.
 +
}}

Latest revision as of 09:27, 6 December 2018

Brief

The Griffith correlation [1] is an empirical correlation which defines:

  • The boundary between the bubble and slug flow[2]
  • The void fraction of gas in bubble flow - gas hold up Hg[2]

Math & Physics

The bubble flow exist when:

\frac{v_g}{v_g + v_L} < L_B [3]
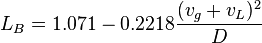L_B = 1.071 - 0.2218 \frac{(v_g+v_L)^2}{D}, with the limit 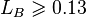L_B \geqslant 0.13 [2]

The gas holdup:

H_g = \frac{1}{2}\ \left ( 1 + \frac{v_g+v_L}{v_s} - \sqrt{ \left ( 1 + \frac{v_g+v_L}{v_s} \right )^2 - 4 \frac{v_g}{v_s}} \right ) [2]

Discussion

Griffith correlation adds a hook to the originally straight Hagedorn and Brown VLP curve.

Nomenclature

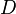D = pipe diameter, ft
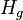H_g = gas holdup factor, dimensionless
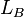L_B = bubble-slug boundary, dimensionless
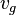v_g = gas velocity, ft/sec
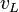v_L = liquid velocity, ft/sec
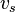v_s = 0.8, slip velocity (difference between average gas and liquid velocities), ft/sec

References

  1. ↑ Griffith, P.; Wallis, G. B. (August 1961). "Two-Phase Slug Flow"Paid subscription required. Journal of Heat Transfer. ASME. 83: 307–320. 
  2. ↑ 2.0 2.1 2.2 2.3 Orkiszewski, J. (June 1967). "Predicting Two-Phase Pressure Drops in Vertical Pipe"Paid subscription required. Journal of Petroleum Technology. SPE. 19 (SPE-1546-PA). 
  3. ↑ Economides, M.J.; Hill, A.D.; Economides, C.E.; Zhu, D. (2013). Petroleum Production Systems (2 ed.). Westford, Massachusetts: Prentice Hall. ISBN 978-0-13-703158-0. 
Retrieved from "https://wiki.pengtools.com/index.php?title=Griffith_correlation&oldid=5464"