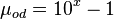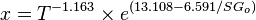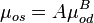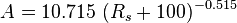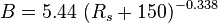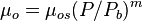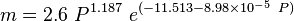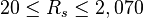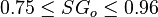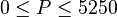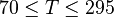Difference between revisions of "Beggs and Robinson Oil Viscosity correlation"

From wiki.pengtools.com
Jump to: navigation, search
(→‎Example. Calculation of the oil viscosity)
(→‎Beggs and Robinson Oil Viscosity correlation)
 
(3 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
__TOC__
 
__TOC__
  
−
== Beggs and Robinson oil viscosity correlation ==
+
== Beggs and Robinson Oil Viscosity correlation ==
  
−
[[Beggs and Robinson correlation|Beggs and Robinson]] is an empirical correlation for the '''oil viscosity''' published in '''1975''' <ref name= BR1975/>.
+
[[Beggs and Robinson Oil Viscosity correlation|Beggs and Robinson]] is an empirical correlation for the '''oil viscosity''' published in '''1975''' <ref name= BR1975/>.
  
 
[[File:Beggs and Robinson.png|thumb|right|400px|link=https://www.pengtools.com/pvtCalculator?paramsToken=b79727e91f05b72cbb6d99afcb588636|Beggs and Robinson oil viscosity correlation in the PVT Software]]
 
[[File:Beggs and Robinson.png|thumb|right|400px|link=https://www.pengtools.com/pvtCalculator?paramsToken=b79727e91f05b72cbb6d99afcb588636|Beggs and Robinson oil viscosity correlation in the PVT Software]]
Line 115: Line 115:
 
  |publisher=Society of Petroleum Engineers
 
  |publisher=Society of Petroleum Engineers
 
  |url=https://www.onepetro.org/book/peh/spe-1987-22-peh
 
  |url=https://www.onepetro.org/book/peh/spe-1987-22-peh
−
  |url-access=subscription
+
  |url-access=registration
 
}}</ref>
 
}}</ref>
 
</references>
 
</references>

Latest revision as of 12:15, 28 September 2020

Beggs and Robinson Oil Viscosity correlation

Beggs and Robinson is an empirical correlation for the oil viscosity published in 1975 [1].

Beggs and Robinson oil viscosity correlation in the PVT Software

Math & Physics

Dead oil viscosity:

\mu_{od} = 10^x-1

where:

x = T^{-1.163} \times e^{(13.108-6.591/SG_{o})}

Saturated oil viscosity (P < Pb):

\mu_{os} = A \mu_{od}^B

where:

A = 10.715\ (R_s + 100)^{-0.515}
B = 5.44\ (R_s + 150)^{-0.338}

Undersaturated oil viscosity (P > Pb):

\mu_{o} = \mu_{os} (P/P_b)^m [2]

where:

m = 2.6\ P^{1.187}\ e^{(-11.513-8.98 \times 10^{-5}\ P)}

Example. Calculation of the oil viscosity

Example source [3]

Input data

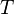T = 137 F°
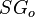SG_o = 0.922 or 22 API
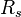R_s = 90 scf/stb

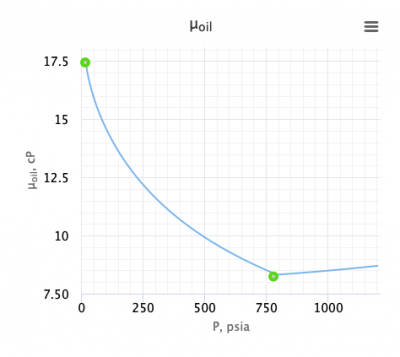
Calculate the saturated oil viscosity?

Solution

x = 1.2658

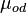\mu_{od} = 17.44 cP

A = 0.719 B = 0.853

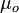\mu_o = 8.24 cP

The solution is available in the online PVT calculator software model at www.pengtools.com

Application range

Description of the Data Used[1]:

20 \le R_s \le 2,070
0.75 \le SG_o \le 0.96
0 \le P \le 5250
70 \le T \le 295

Number of oil systems = 600
Number of dead oil observations = 460
Number of live oil observations = 2,073

Nomenclature

A = coefficient
B = coefficient
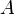m 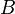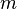= coefficient
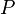P = pressure, psia
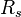R_s = solution gas-oil ratio, scf/stb
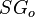SG_o = oil specific gravity, dimensionless
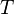T = temperature, °F
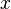x = coefficient
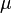\mu = viscosity, cP

Subscripts

b - bubble point
od - dead oil
os - saturated oil
o - undersaturated oil

References

  1. ↑ 1.0 1.1 Beggs, H. D.; Robinson, J. R. (September 1975). "Estimating the Viscosity of Crude Oil Systems"Free registration required. Journal of Petroleum Technology. 27(09) (SPE-5434-PA). 
  2. ↑ Vasquez, M.; Beggs, H.D. (1980). "Correlations for Fluid Physical Property Prediction."Free registration required. Society of Petroleum Engineers (SPE-6719-PA). 
  3. ↑ Beggs, H. Dale (1987). Oil System Correlations (1987 PEH Chapter 22)Free registration required. Society of Petroleum Engineers. 
Retrieved from "https://wiki.pengtools.com/index.php?title=Beggs_and_Robinson_Oil_Viscosity_correlation&oldid=7022"