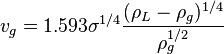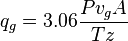Difference between revisions of "Liquid loading"
From wiki.pengtools.com
(→Nomenclature) |
|||
| Line 12: | Line 12: | ||
=== Nomenclature === | === Nomenclature === | ||
| − | :<math> | + | :<math> A </math> = flow area, ft^2 |
| + | :<math> q_g </math> = gas rate, MMscf/d | ||
| + | :<math> P </math> = flowing pressure, psia | ||
| + | :<math> \rho_g </math> = gas density, lbm/ft3 | ||
| + | :<math> \rho_L </math> = liquid density, lbm/ft3 | ||
:<math> \sigma </math> = surface tension, dyne/cm | :<math> \sigma </math> = surface tension, dyne/cm | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math> T </math> = flowing temperature, °R | :<math> T </math> = flowing temperature, °R | ||
| + | :<math> v_g </math> = gas velocity, ft/sec | ||
:<math> z </math> = gas compressibility factor at flowing P & T | :<math> z </math> = gas compressibility factor at flowing P & T | ||
Revision as of 13:02, 15 March 2017
Brief
Liquid loading is a phemonenon when the gas phase does't provide sufficient transport energy to lift the liquids out of the well.
Math & Physics
The minimum gas velocity to remove the liquid equation:
The minimum gas rate to remove the liquid equation:
Nomenclature
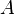 = flow area, ft^2
= flow area, ft^2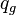 = gas rate, MMscf/d
= gas rate, MMscf/d = flowing pressure, psia
= flowing pressure, psia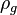 = gas density, lbm/ft3
= gas density, lbm/ft3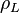 = liquid density, lbm/ft3
= liquid density, lbm/ft3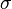 = surface tension, dyne/cm
= surface tension, dyne/cm = flowing temperature, °R
= flowing temperature, °R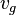 = gas velocity, ft/sec
= gas velocity, ft/sec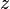 = gas compressibility factor at flowing P & T
= gas compressibility factor at flowing P & T
References
Turner, R. G., Hubbard, M. G., and Dukler, A. E. (1969) “Analysis and Prediction of Minimum Flow Rate for the Continuous Removal of Liquids from Gas Wells,” Journal of Petroleum Technology, Nov. 1969. pp. 1475–1482.