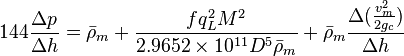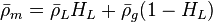Difference between revisions of "Hagedorn and Brown correlation"
From wiki.pengtools.com
(→Workflow) |
|||
| Line 5: | Line 5: | ||
It doesn't distinguish between the flow regimes. | It doesn't distinguish between the flow regimes. | ||
| − | == | + | == Theory == |
:<math> 144 \frac{\Delta p}{\Delta h} = \bar \rho_m + \frac{f q_L^2 M^2}{2.9652 \times 10^{11} D^5 \bar \rho_m} + \bar \rho_m \frac{\Delta{(\frac{v_m^2}{2g_c}})}{\Delta h}</math> | :<math> 144 \frac{\Delta p}{\Delta h} = \bar \rho_m + \frac{f q_L^2 M^2}{2.9652 \times 10^{11} D^5 \bar \rho_m} + \bar \rho_m \frac{\Delta{(\frac{v_m^2}{2g_c}})}{\Delta h}</math> | ||
| − | :<math> \bar \rho_m = \bar \rho_L H_L + \bar \rho_g (1 - H_L)</math> | + | :<math> \bar \rho_m = \bar \rho_L H_L + \bar \rho_g (1 - H_L)</math> |
== Block Diagram == | == Block Diagram == | ||
Revision as of 14:42, 14 March 2017
Contents
Info
Hagedorn and Brown is an empirical two-phase flow correlation published in 1965.
It doesn't distinguish between the flow regimes.